Kirchoff's Loop Rule Involving 2 Resistors and a Capacitor

[Niall Kennedy]

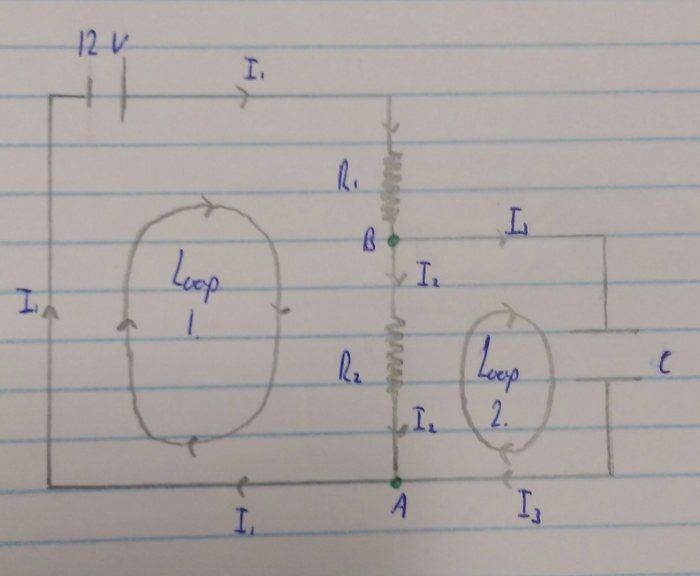
A 5μF capacitor is connected in parallel with a 2MΩ resistor and the combination is then connected in series with a 1MΩ resistor through a switch to a 12V battery. Find the time taken for the voltage across the capacitor to rise from zero initial value to 2V after the switch is closed.From what I understand this requires Kirchoff's loop and junction rules which is okay up until I hit the voltage across the capacitor which is where I get stuck.Here's the diagram I made to work from, hopefully it's right:

 

[Passionate Eng]

Vc(t)=Forced response + Transient response
forced response"steady state response" is found at time equals infinity at which the capacitor becomes open circuit
here it is : 12*(2/3)=8 volts ... voltage division
____________
transient response (after solving a differential equation) is : A*exp(-t/taw) where "taw" is the time constant RC
then you can find A by substituting the initial condition which is the initial voltage of the capacitor at time t<0
here A is -8 volts
___________
now: Vc(t)=8 - 8*exp(-t/taw)
and you can easily find the time at which the voltage reaches 2 volts by sitting Vc(t)=2

 

[Niall Kennedy]

Thanks for the help, I was going to go around it that way but my issue was that taw = RC and I'm not sure what taw is since there's a resistor in series and one in parallel

 

[Passionate Eng]

R is the parallel combination of R1 and R2

 

[gneill]

Hint: Think Thevenin equivalent.