Lachlan's question via email about the Bisection Method

In summary, the Bisection Method was used to solve the equation $\displaystyle 8\cos{\left( x \right) } = \mathrm{e}^{-x/7} $ by rewriting it as $\displaystyle 8\cos{ \left( x \right) } - \mathrm{e}^{-x/7} = 0 $ and using the function $\displaystyle f\left( x \right) = 8\cos{ \left( x \right) } - \mathrm{e}^{-x/7} $. Four iterations were performed within the interval $\displaystyle x \in \left[ 1.35, 1.6 \right] $ to find an
  • #1
Prove It
Gold Member
MHB
1,465
24
Consider the equation $\displaystyle 8\cos{\left( x \right) } = \mathrm{e}^{-x/7} $.

Perform four iterations of the Bisection Method to find an approximate solution in the interval $\displaystyle x \in \left[ 1.35, 1.6 \right] $.

The Bisection Method is used to solve equations of the form $\displaystyle f\left( x \right) = 0 $, so we need to rewrite the equation as $\displaystyle 8\cos{ \left( x \right) } - \mathrm{e}^{-x/7} = 0 $. Thus $\displaystyle f\left( x \right) = 8\cos{ \left( x \right) } - \mathrm{e}^{-x/7} $.

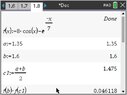
I have used my CAS to solve this problem. Note that the calculator must be in Radian mode.

View attachment 9640

View attachment 9641

View attachment 9642

So our solution is $\displaystyle x \approx c_4 = 1.45938 $.
 

Attachments

  • bm1.jpg
    bm1.jpg
    23.4 KB · Views: 117
  • bm2.jpg
    bm2.jpg
    21.9 KB · Views: 124
  • bm3.jpg
    bm3.jpg
    21.6 KB · Views: 105
Mathematics news on Phys.org
  • #2
I checked your calculations using Excel, and they agree. After a couple more iterations I get x≈1,4701171875.
 

FAQ: Lachlan's question via email about the Bisection Method

What is the Bisection Method?

The Bisection Method is a numerical method used to find the root of a function. It involves repeatedly dividing the interval in which the root is suspected to be located and narrowing down the interval until the root is found.

How does the Bisection Method work?

The Bisection Method works by first selecting an interval in which the root is suspected to be located. Then, the midpoint of the interval is calculated and used to determine which half of the interval the root is in. This process is repeated until the root is found within a desired level of accuracy.

What are the advantages of using the Bisection Method?

The Bisection Method is relatively simple to implement and does not require any knowledge of the derivative of the function. It also guarantees convergence to the root as long as the function is continuous and changes sign within the chosen interval.

What are the limitations of the Bisection Method?

The Bisection Method can be slow to converge compared to other numerical methods. It also requires an initial interval in which the root is suspected to be located, which may not always be easy to determine.

In what situations is the Bisection Method commonly used?

The Bisection Method is commonly used when finding the root of a function is difficult or impossible to do analytically. It is also useful when the function is continuous and changes sign within a given interval.

Similar threads

MHB Lachlan's question via email about the Bisection Method
Replies
1
Views
9K
MHB Alexander's question via email about Newton's Method
Replies
1
Views
10K
MHB Hayldiburasomas' question via email about Secant Method
Replies
1
Views
10K
MHB Aidan's question via email about Fourier Transforms (2)
Replies
1
Views
10K
MHB Aidan's question via email about Fourier Transforms
Replies
1
Views
9K
MHB Jun's question via email about Laplace Transform
Replies
2
Views
10K
MHB Mahesh's question via email about Laplace Transforms (2)
Replies
1
Views
10K
MHB Massaad's question via email about Laplace Transforms
Replies
1
Views
9K
MHB Oscar's question via email about solving a DE using Laplace Transforms
Replies
0
Views
9K
MHB Alexander's question via email about Laplace Transforms
Replies
1
Views
10K

Hot Threads

Recent Insights

Back
Top