Ladder problem (statics) with 2 sources of friction

[natasha13100]

Homework Statement

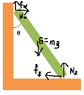
A uniform ladder of mass m and length L rests against the wall as shown. The coefficients of static friction between the floor and the ladder and between the wall and the ladder are equal to each other (μ). What is the maximum value of angle θ that the ladder can make with the wall without sliding? (Use m for m, L for L, mu for μ, and arcsin, arccos, and arctan for the inverse trig functions.)

Homework Equations

f(friction)≤μN(normal force)
t(torque)=r(moment arm)Fsinθ
G=mg

The Attempt at a Solution

FBD is attached

because the ladder is not moving
t=-mgLsinθ/2+N_fLsinθ-μN_fLcosθ=0
F_x=N_w-f_f=0
F_y=N_f+f_w-mg=0

Solve t for N_f
N_fLsinθ-μN_fLcosθ=mgLsinθ/2
N_ftanθ-μN_f=mgtanθ/2
N_f=mgtanθ/(2(tanθ-μ))

When θ is at its maximum without the ladder slipping, f=μN.
f_f=μmgtanθ/(2(tanθ-μ))
Solve F_xfor N_w
N_w=μmgtanθ/(2(tanθ-μ))
Also f_w=μ²mgtanθ/(2(tanθ-μ))

Solve F_y for θ.
mgtanθ/(2(tanθ-μ))+μ²mgtanθ/(2(tanθ-μ))=mg
tanθ/(2(tanθ-μ))+μ²tanθ/(2(tanθ-μ))=1
tanθ=2(tanθ-μ)/(1+μ²)
(tanθ-μ)/tanθ=(1+μ²)/2
1-μ/tanθ=(1+μ²)/2
μ/tanθ=1-(1+μ²)/2
tanθ=μ/(1-(1+μ²)/2)
θ=arctan(μ/(1-(1+μ²)/2))

 

[TSny]

Your work looks good to me. You can simplify your answer a bit.

[Would there be a solution if $\mu > 1$? For most substances $\mu < 1$, but there exist substances for which $\mu > 1$.]

 

[natasha13100]

Oh yes it is. I finally figured out where my mistake was. I've been trying to simplify the answer and it would come out wrong. I would get an answer like 2/(1+μ). A simple algebra mistake. Thanks. :) By the way, if I am thinking correctly, the angle would exist but it would be extremely small.