kidsasd987
- 142
- 4
Hi, I have a question about lagrange multiplier
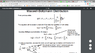
Let's say we are given with the following constraints
Σ{Ni}=N and Σ{NiEi}=total energy. N and total energy are constants by definition.
if we take the derivative with respect to Nj,
∂Σ{Ni}/∂Nj=∂N/∂Nj
where i=j, ∂Σ{Ni}/∂Nj=1 and ∂N/∂Nj = 0 because N is constant.
On slide 14, it says ∂N/∂Nj = 0 while ∂Σ{Ni}/∂Nj=1 with the preceding constraint Σ{Ni}=N.
Then, we can conclude
∂Σ{Ni}/∂Nj= ∂N/∂Nj=0.
This is quite ambiguous to me.
if we assume we have a constraint x1+x2+x3..+xn=const.
partial of this constraint with respect to xj will be 1=0 therefore it is contradiction.
how shoud I interpret this?
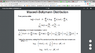
Let's say we are given with the following constraints
Σ{Ni}=N and Σ{NiEi}=total energy. N and total energy are constants by definition.
if we take the derivative with respect to Nj,
∂Σ{Ni}/∂Nj=∂N/∂Nj
where i=j, ∂Σ{Ni}/∂Nj=1 and ∂N/∂Nj = 0 because N is constant.
On slide 14, it says ∂N/∂Nj = 0 while ∂Σ{Ni}/∂Nj=1 with the preceding constraint Σ{Ni}=N.
Then, we can conclude
∂Σ{Ni}/∂Nj= ∂N/∂Nj=0.
This is quite ambiguous to me.
if we assume we have a constraint x1+x2+x3..+xn=const.
partial of this constraint with respect to xj will be 1=0 therefore it is contradiction.
how shoud I interpret this?