You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
What is Lagrange: Definition and 540 Discussions
Joseph-Louis Lagrange (born Giuseppe Luigi Lagrangia or Giuseppe Ludovico De la Grange Tournier; 25 January 1736 – 10 April 1813), also reported as Giuseppe Luigi Lagrange or Lagrangia, was an Italian mathematician and astronomer, later naturalized French. He made significant contributions to the fields of analysis, number theory, and both classical and celestial mechanics.
In 1766, on the recommendation of Swiss Leonhard Euler and French d'Alembert, Lagrange succeeded Euler as the director of mathematics at the Prussian Academy of Sciences in Berlin, Prussia, where he stayed for over twenty years, producing volumes of work and winning several prizes of the French Academy of Sciences. Lagrange's treatise on analytical mechanics (Mécanique analytique, 4. ed., 2 vols. Paris: Gauthier-Villars et fils, 1788–89), written in Berlin and first published in 1788, offered the most comprehensive treatment of classical mechanics since Newton and formed a basis for the development of mathematical physics in the nineteenth century.
In 1787, at age 51, he moved from Berlin to Paris and became a member of the French Academy of Sciences. He remained in France until the end of his life. He was instrumental in the decimalisation in Revolutionary France, became the first professor of analysis at the École Polytechnique upon its opening in 1794, was a founding member of the Bureau des Longitudes, and became Senator in 1799.
View More On Wikipedia.org
In 1766, on the recommendation of Swiss Leonhard Euler and French d'Alembert, Lagrange succeeded Euler as the director of mathematics at the Prussian Academy of Sciences in Berlin, Prussia, where he stayed for over twenty years, producing volumes of work and winning several prizes of the French Academy of Sciences. Lagrange's treatise on analytical mechanics (Mécanique analytique, 4. ed., 2 vols. Paris: Gauthier-Villars et fils, 1788–89), written in Berlin and first published in 1788, offered the most comprehensive treatment of classical mechanics since Newton and formed a basis for the development of mathematical physics in the nineteenth century.
In 1787, at age 51, he moved from Berlin to Paris and became a member of the French Academy of Sciences. He remained in France until the end of his life. He was instrumental in the decimalisation in Revolutionary France, became the first professor of analysis at the École Polytechnique upon its opening in 1794, was a founding member of the Bureau des Longitudes, and became Senator in 1799.
View More On Wikipedia.org
-
M
Lagrange method problem: Multiple Spring-Mass System
4 I am working on problem c and I'm not sure if I'm doing it right, please can you help me understand if I am on the right lines? I want to get a better understanding of lagrange method problems Here is my working: I have labelled ##k_1,k_2,k_3,k_4, k_5## left to right Generalised...- Motorbiker
- Thread
-
- Tags
- generalized Lagrange Stiffness
- Replies: 22
- Forum: Advanced Physics Homework Help
-
M
Euler- Lagrange equation proof
For this problem, The solution is, However, I have a question about the solution. Does someone please know why they write out ##\frac{dF}{dx} = \frac{\partial F}{\partial y}y' + \frac{\partial F}{\partial y'}y''## since we already know that ##\frac{dF}{dx} = 0##? Thanks!- member 731016
- Thread
- Replies: 2
- Forum: Introductory Physics Homework Help
-
M
Lagrange equation for block and incline
For this problem, Does someone please know where the term highlighted in blue came from? Thanks!- member 731016
- Thread
- Replies: 13
- Forum: Introductory Physics Homework Help
-

Generalized coordinates and the Lagrangian
So I think the mass can only move in two "coordinates" the axis of which the mass is connected to ##k_1## and the axis connecting it to ##k_2##. Therefore, the D.O.F is 2. I don't understand what it the meaning of "variables of integration" What does it mean? Apart from that, I attempted to...- GLD223
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-

I Requirement of Holonomic Constraints for Deriving Lagrange Equations
While deriving the Lagrange equations from d'Alembert's principle, we get from $$\displaystyle\sum_i(m\ddot x_i-F_i)\delta x_i=0\tag{1}$$ to $$\displaystyle\sum_k (\frac {\partial\mathcal L}{\partial\ q_k}-(\frac d {dt}\frac {\partial\mathcal L}{\partial\dot q_k}))\delta q_k=0\tag{2}$$ However...- deuteron
- Thread
- Replies: 1
- Forum: Classical Physics
-
O
Modifying Euler-Lagrange equation to multivariable function
I'm confused on how to derive the multidimensional generalization for a multivariable function. Everything makes sense here except the line, $$ \frac{\delta S}{\delta \psi} = \frac{\partial L}{\partial \psi} - \frac{d}{dx} \frac{\partial L}{\partial(\frac{\partial \psi}{\partial x})} -...- offscene
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-
I Help with Euler Lagrange equations: neighboring curves of the extremum
I tried writing this out but I think there is a bug or something as its not always displaying the latex, so sorry for the image. I have gone through various sources and it seems that the reason for u being small varies. Sometimes it is needed because of the taylor expansion, this time (below) is...- Reuben_Leib
- Thread
- Replies: 5
- Forum: Classical Physics
-
A
My Epic Fail at Deriving an Equation with Lagrange
Here is my epic fail at trying to derive the equation using Lagrange (this was my first time trying to use lagrangian mechanics except for when I memorized the derivation for a pendulum) $$L = \frac{m \dot r^2}{2} - \frac{k q_1 q_2}{r}$$ $$\frac{\partial L}{\partial r} = \frac{k q_1 q_2}{r^2}$$...- Arm
- Thread
- Replies: 16
- Forum: Advanced Physics Homework Help
-
H
I Momentum and Action: Understanding Lagrangian Mechanics
Hi, In my book I have and expression that I don't really understand. Using the definition of action ##\delta S = \frac{\partial L}{\partial \dot{q}} \delta q |_{t_1}^{t_2} + \int_{t_1}^{t_2} (\frac{\partial L}{\partial q} - \frac{d}{dt} \frac{\partial L}{\partial \dot{q}}) \delta q dt## Where L...- happyparticle
- Thread
-
- Tags
- Hamiltonian Lagrange Momentum
- Replies: 5
- Forum: Classical Physics
-

I How to find the equation of motion using Lagrange's equation?
Good morning, I'm not a student but I'm curious about physics. I would like to calculate the equation of motion of a system using the Lagrangian mechanics. Suppose a particle subjected to some external forces. From Wikipedia, I found two method: 1. using kinetic energy and generalized forces...- Pironman
- Thread
- Replies: 13
- Forum: Classical Physics
-

Study of harmonic motion of a liquid in a V shaped tube
A V-shaped tube with a cross-section A contains a perfect liquid with mass density and length L plus and the angles between the horizontal plane and the tube arms as shown in the attached figure. We displace the liquid from its equilibrium position with a distance and without any initial... -

Is it possible to find Tensional force from Lagrange?
Lagrangian principle is easier to solve any kind of problem. But we always "forget" (not really. But we don't take it into account directly.) of Tension in a system when looking at Lagrangian. But some questions say to find Tension. Since we can get the equation of motion from Newton's 2nd law...- mcconnellmelany
- Thread
-
- Tags
- Force Lagrange Lagrangian Tension
- Replies: 13
- Forum: Advanced Physics Homework Help
-
J
A Can Newton's Method Solve Freer Motion?
Hello everyone, my question is, if there is a case, where you can't you Langrange (1 or 2) but only Newton to solve the equation of motion? My guess is, that it might be, when we have no restrictions at all, so a totally free motion. Does anybody know? -

Cartesian and polar coordinate in Simple pendulum, Euler-Lagrange
$$L = \frac {mv^2}{2} - mgy$$ It is clear that ##\dot{x}=\dot{\theta}L## and ##y=-Lcos \theta##. After substituting these two equations to Lagrange equation, we will get the answer by simply using this equation: $$\frac {d} {dt} \frac {∂L}{∂\dot{\theta}} - \frac {∂L}{∂\theta }= 0$$ But, What if...- Father_Ing
- Thread
- Replies: 4
- Forum: Introductory Physics Homework Help
-

B Questions about Lagrange points in the Pluto / Charon system
Hello. With the recent interest in the JWST orbiting at the L2 Lagrange point of the Earth - Moon system, I was wondering about the dynamics of the Pluto - Charon system. Specifically, the barycentre of that system. This barycentre lies at a point in space between these two bodies. Does...- Cerenkov
- Thread
- Replies: 2
- Forum: Astronomy and Astrophysics
-

Finding Lagrange Point L2: Gravity and Harmonics
So we are finding the L2 Lagrange point, specifically the distance from the earth, or d in this instance. I have used the equation above and I have come out with 1.5 * 10^9 meters as d, or L2's distance from the earth. Can anyone verify this, is the equation correct and is my final distance... -

Can't get Lagrange multiplier to work in a single exercise
So I understand the concept of lagrange multiplier but I fail at every single execise I encounter anyways. Because you always end up with unsolvable equations of x^3yzb3gh + 37y^38x^3 + k^5x = 0 Anways here's my stupid attempt: Instead of doing $$grad(f) + \lambda grad(g) = 0$$ I solve $$...- Addez123
- Thread
- Replies: 16
- Forum: Calculus and Beyond Homework Help
-
T
A Euler Lagrange and the Calculus of Variations
Good Morning all Yesterday, as I was trying to formulate my confusion properly, I had a series of posts as I circled around the issue. I can now state it clearly: something is wrong :-) and I am so confused :-( Here is the issue: I formulate the Lagrangian for a simple mechanical system...- Trying2Learn
- Thread
- Replies: 2
- Forum: Classical Physics
-

I Lagrangian mechanics - generalised coordinates question
I think I undeerstand Lagrangian mechanics but I have a question that will help to clarify some concepts. Imagine I throw a pencil. For that I have 5 generalised coordinates (x,y,z and 2 rotational). When I express Kinetic Energy (T) as: $$T = 1/2m\dot{x^{2}}+1/2m\dot{y^{2}}+1/2m\dot{z^{2}} +...- curiousPep
- Thread
- Replies: 4
- Forum: Mechanics
-

A Einbein as Lagrange Multiplier: How Does it Work?
Let ##g_{\mu \nu}(x)## be a time-independent metric. A photon following a curve ##\Gamma## has action\begin{align*} I[x,e]= \dfrac{1}{2} \int_{\Gamma} e^{-1}(\lambda) g_{\mu \nu}(x)\dot{x}^{\mu} \dot{x}^{\nu} d\lambda \end{align*}with ##e(\lambda)## an independent function of ##\lambda## (an...- ergospherical
- Thread
- Replies: 3
- Forum: Special and General Relativity
-
T
A Hamilton's Method with Lagrange Equation and Constraint
Good Morning I am "comfortable" with formulating Hamilton's Principle with a Lagrangian (KE - PE), conducting the calculus of variations and obtaining the Euler Lagrange Equations. Advanced mathematical theory, is beyond me. I also have a minimal understanding of using Lagrange multipliers...- Trying2Learn
- Thread
- Replies: 1
- Forum: Classical Physics
-
T
B Delta-v from Lagrange points to lunar surface?
What is the delta-v requirements from each of the Earth-Moon lagrange points to landing on the lunar surface? What would be the best software I could use to visualise and calculate that kind of thing? Thanks.- Treva31
- Thread
- Replies: 5
- Forum: Astronomy and Astrophysics
-
M
MHB Optimization - Lagrange multipliers : minimum cost/maximum production
Hey! :giggle: Business operates on the basis of the production function $Q=25\cdot K^{1/3}\cdot L^{2/3}$ (where $L$ = units of work and $K$ = units of capital). If the prices of inputs $K$ and $L$ are respectively $3$ euros and $6$ euros per unit, then find : a) the optimal combination of... -
A
Centaur Mass for Jupiter's 4th Lagrange Point
Hi again How much mass would a centaur need to have Lagrange points? (is a centaur of this size plausible?) In the story I'm working on a massive centaur passes near Jupiter's 4th Lagrange point, such that the centaur's Lagrange point and Jupiter's overlap. Could the centaur come at an angle...- AllanR
- Thread
-
- Tags
- Lagrange
- Replies: 2
- Forum: Sci-Fi Writing and World Building
-

Symmetries in Lagrangian Mechanics
In Classical Mechanics by Kibble and Berkshire, in chapter 12.4 which focuses on symmetries and conservation laws (starting on page 291 here), the authors introduce the concept of a generator function G, where the transformation generated by G is given by (equation 12.29 on page 292 in the text)... -

I Can Lagrange multipliers be used to find a function?
Problem statement : Let ##f\in C^\infty ([-1;1])## with ##f(1)=f(-1)=0## and ##\int_{-1}^1f(x)dx=1## Which curve has the lowest (maximal) absolute slope ? Attempt : Trying to minimize ##f′(x)−\lambda f″(x)## with Lagrange multipliers but to find f not x ? I got... -
A
The Lagrange equations from mechanics
I was having a doubt about the Lagrangian mechanics. Possible we can derive the lagranges equations of by extremisation principle of action, that is assume we already guess what is the lagrangian of the systeme. I say that minimisation procedure rely on assume a lagrangian, and then show it... -

A Lagrange with Higher Derivatives (Ostrogradsky instability)
In class our teacher told us that, if a Lagrangian contain ##\ddot{q_i}## (i.e., ##L(q_i, \dot{q_i}, \ddot{q_i}, t)##) the energy will be unbounded from below and it can take any lower values (in other words be unstable). In this type of systems can we show that the energy is conserved ? Or in...- Arman777
- Thread
- Replies: 3
- Forum: Classical Physics
-
L
MHB Simplifying lagrange interpolation polynomial
Now $\sum_{i=0}^{10}(x_{i}+1) L _{10,i}(5) = (x_{0}+1) L _{10,0}(5) + (x_{1}+1) L _{10,1}(5) + ... + (x_{10}+1) L _{10,10}(5)$ Which I can further decompose into $\frac{(x_{0}+1)(5-x_{1})(5-x_{2})...(5-x_{10})}{(x_{0}-x_{1})(x_{0}-x_{2})...(x_{0}-x_{10})} +...- lemonthree
- Thread
- Replies: 1
- Forum: General Math
-
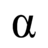
Finding the Equation System of a Complex Mechanism: Using Lagrange Formalism
Summary:: equation system of complex mechanism need to be done. Lagrange Formalism could be helpfull to do it but small errors could all destroy .. Hi everyone, I tried to find the equation system of the joined Mechanism (4 DoF). I think there is a mistake but I am not sure where is it . I...- Nagui
- Thread
- Replies: 1
- Forum: Engineering and Comp Sci Homework Help
-
S
I Linearization of Lagrange equations
l am italian student from Milan university, so sorry for my bad english. l am studying lagrange meccanics. We are linearizating lagrange equations. Here l don't understand how you can expand A matrix, how the function f is derivable, how the inverse matrix A is expanded? l am expanding with q0...- stefano77
- Thread
-
- Tags
- Lagrange Linearization
- Replies: 5
- Forum: Classical Physics
-

Difficulty with Lagrange multipliers in Kardar's Statistical Physics book
Alright, so I did some progress and then I got stuck. After some time I went to check the solution. Up to some point, it's all well and good: I understand everything that is happening up to the point where he takes the partial derivative of S wrt ρ(Γ). I don't understand how he gets the...- AndreasC
- Thread
- Replies: 4
- Forum: Advanced Physics Homework Help
-
Euler Lagrange equations in continuum
OK I've been stuck for a while in how to derive ##(1)##, so I better solve a simplified problem first: We work with Where $$\mathscr{L} = \mathscr{L}(\phi_a (\vec x, t), \partial_{\mu} \phi_a (\vec x, t)) \tag{3}$$ And ##(3)## implies that ##\mathscr{L}(\vec x, t)## We know that...- JD_PM
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-

Lagrange Multipliers and Energy Loss Question
Constraint: ##I=I_{1}+I_{2}## ##P_{diss,R_{1}}=I_{1}^{2}R_{1}##;##P_{diss,R_{2}}=I_{2}^{2}R_{2}## We want to minimize ##P_{diss,TOT}=I_{1}^{2}R_{1}+I_{2}^{2}R_{2}## $$f(I_{1},I_{2})=I_{1}^{2}R_{1}+I_{2}^{2}R_{2};g(I_{1},I_{2})=I_{1}+I_{2}=I(constraint)$$ $$\nabla f= \left \langle \frac{\partial...- cwill53
- Thread
- Replies: 19
- Forum: Introductory Physics Homework Help
-
T
Finding Specific Extrema when grad(F)=constant & Lagrange Gives y=-z/2
I found that f= x -2yz. To maximize f, I can first inspect the solutions to grad(F)=0. z=y=0 pops out, but I'm not sure what to do with the x-component equaling 1. Do we just include (x,0,0) as a solution? I think the problem wants specifics though, based on what I've seen previously from...- The Head
- Thread
- Replies: 10
- Forum: Calculus and Beyond Homework Help
-

Lagrange method to find extremes
ƒ(x,y) = 3x + y x² + 2y² ≤ 1 It is easy to find the maximum, the really problem is find the minimum, here is the system: (3,1) = λ(2x,4y) x² + 2y² ≤ 1 how to deal with the inequality?- LCSphysicist
- Thread
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-

I Lagrangian and the Euler Lagrange equation
I am new to Lagrangian mechanics and I am unable to comprehend why the Euler Lagrange equation works, and also what really is the significance of the lagrangian.- Hamiltonian
- Thread
- Replies: 2
- Forum: Classical Physics
-
T
Small deviations from equilibrium and Lagrange multipliers
According to the book "Principles of Statistical Mechanics" by Amnon Katz, page 123, ##\alpha## must be such that ##\exp ( -\alpha N ) ## can be expanded in powers of ##\alpha## with only the first order term kept. Is this the necessary and sufficient condition for small deviations from...- Ted Ali
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-
T
Euler Lagrange equation and a varying Lagrangian
Hello, I have been working on the three-dimensional topological massive gravity (I'm new to this field) and I already faced the first problem concerning the mathematics, after deriving the lagrangian from the action I had a problem in variating it Here is the Lagrangian The first variation...- Tamin Ayoub
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-

A The tautological 1-form: Lagrange vs. Hamilton formalism
Classical mechanics is based on conservation laws which represent the symmetries of spacetime. The lagrangian function L is a function of position and velocity while the hamiltonian is a function of position and momentum. The velocity and momentum descriptions are related by a legendre...- PGaccount
- Thread
- Replies: 27
- Forum: Classical Physics
-
Lagrange equations of the first kind
We cannot make it anyhow- saRisky
- Thread
-
- Tags
- Lagrange
- Replies: 1
- Forum: Introductory Physics Homework Help
-

How to model a function of a box's volume using Lagrange multiplier methods
I started to understand how to apply Lagrange multiplier methods. But, for problem like this, I have difficulty to build the function to describe the volume that will be maximized. For the second question, I know from the example (in ML Boas) that ##V=8xyz## becase (x,y,z) is in the 1st octant...- agnimusayoti
- Thread
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
Z
Lagrange equations: Two blocks and a string
I've problems understanding why the kinetic energy of the string is only $$T_{string}=\frac{1}{2}m\dot{y} $$ Why the contribution of the string in the horizontal line isn't considered?- Zamarripa
- Thread
- Replies: 9
- Forum: Advanced Physics Homework Help
-

I Question about Lagrange multipliers
I'm having some trouble understanding the following proof (##a_{ik}## and ##b_{ik}## are constants) Shouldn't it be ##a_{ik}q_iq_k - \frac 1 {\lambda} (b_{ik}q_iq_k-1)## ? (Summation convention is used) Thanks Ric- dRic2
- Thread
- Replies: 13
- Forum: General Math
-

What Are the Dimensions of the Least Expensive Conical Frustum Container?
Hi there! Kindly help me to solve the problem below. A company is using frustum of a cone containers for their products. What are the dimensions of the least expensive container that can hold 300 cubic cm? Use Lagrange Multipliers to solve the problem. Thanks.- Morfe
- Thread
- Replies: 12
- Forum: Calculus and Beyond Homework Help
-

D'Alembert's principle and the work done by constraint forces
From what I understand, constraint forces do no work because they are perpendicular to the allowed virtual displacements of the system. However, if you consider an unbalanced Atwood machine, in which both masses are accelerating in opposite directions, you'll find that the tension force of the...- polytheneman
- Thread
- Replies: 6
- Forum: Mechanics
-
How Do You Calculate the Acceleration of a Box on Banked Wheels?
A homogen box with the mass M rolls without sliding on two round wheels. The wheels with mass mass m are also homogen and roll without sliding, on top of the banked Surface. We use Gravitation g. Find the accelration xM of the box I don't know which solution is correct. i got 0.67 m for xM...- tamim94
- Thread
- Replies: 1
- Forum: Introductory Physics Homework Help
-
Deriving the Equation of Motion out of the Action
Exercise statement: Given the action (note ##G_{ab}## is a symmetric matrix, i.e. ##G_{ba} = G_{ab}##): $$S = \int dt \Big( \sum_{ab} G_{ab} \dot q^a\dot q^b-V(q)\Big)$$ Show (using Euler Lagrange's equation) that the following equation holds: $$\ddot q^d +...- JD_PM
- Thread
- Replies: 15
- Forum: Advanced Physics Homework Help
-
F
Horizontal Circular Motion With Lagrange
In the situation described in the problem, the mass is moving on a horizontal circular path with constant velocity. Wouldn’t this make L and U both constant? Then the Lagrange equation would give 0 = 0, which isn’t what I’m looking for. Any help would be appreciated.- Fascheue
- Thread
- Replies: 5
- Forum: Introductory Physics Homework Help