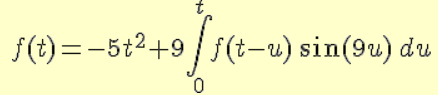Laplace Convolution: f(t)=-5t^2+9
- Context: MHB
- Thread starter Alex2124
- Start date
-
- Tags
- Convolution Laplace
Click For Summary
The discussion centers on the Laplace convolution of the function f(t) = -5t² + 9, specifically analyzing the integral equation involving the sine function. The Laplace transform is applied, yielding the equation F(s) = -5(2/s³) + 9F(s)(9/(s² + 81)). This formulation combines a quadratic function with an integral, prompting inquiries about the representation and implications of f(t) in relation to the integral. The participants express interest in further context regarding the function's significance and its mathematical properties.
PREREQUISITES- Understanding of Laplace transforms and their properties
- Familiarity with integral calculus and convolution operations
- Knowledge of trigonometric functions, specifically sine
- Basic concepts of differential equations and their solutions
- Explore the properties of Laplace transforms in detail
- Study convolution integrals and their applications in differential equations
- Investigate the significance of quadratic functions in mathematical modeling
- Learn about the applications of Laplace transforms in engineering and physics
Mathematicians, engineering students, and anyone interested in advanced calculus and differential equations will benefit from this discussion, particularly those focusing on Laplace transforms and convolution techniques.
Similar threads
- · Replies 1 ·
- · Replies 10 ·
- · Replies 1 ·
- · Replies 10 ·
- · Replies 1 ·
- · Replies 2 ·
- · Replies 4 ·
- · Replies 2 ·
- · Replies 1 ·
- · Replies 4 ·