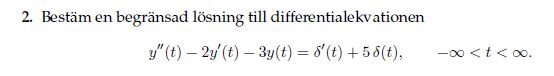Discussion Overview
The discussion revolves around the application of the Laplace transform and its inverse in solving a differential equation, particularly focusing on the interpretation of terms involving delta functions and step functions in the context of the solution.
Discussion Character
- Technical explanation, Conceptual clarification, Debate/contested
Main Points Raised
- One participant questions why the inverse Laplace transform of $$\frac{-1}{s+1} + \frac{2}{s-3}$$ does not yield $$-e^{-t} + 2e^{3t}$$ for $$t>0$$.
- Another participant suggests that the presence of delta functions on the right side of the equation alters the conditions under which the transforms are valid, implying that step functions are necessary for the solution.
- A further inquiry is made regarding the specific values that determine the application of step functions and how they are utilized in the solution.
- There is a question raised about the meanings of "\delta(x)" and "\delta'(x)", indicating a potential need for clarification on these concepts.
Areas of Agreement / Disagreement
Participants do not appear to reach consensus, as there are competing views regarding the role of delta functions and the conditions for the validity of the inverse Laplace transform.
Contextual Notes
The discussion highlights the dependence on the definitions of delta functions and the conditions under which step functions apply, which remain unresolved.