Laplace Operator: Vector Dot Product & 2nd Derivative

[ameeno97]

Hi guys

The Laplace Operator

The Laplace operator is defined as the dot product (inner product) of two gradient vector operators:

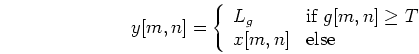
When applied to f(x,y), this operator produces a scalar function:

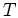
My question is how a vector dot product ( del operator vector dot product del operator vector) will result in the second derivative!? shouldn't it be del operator squared?

 

[Char. Limit]

If you think about the dot product, which says that a dot b = a_1 b_1 + a_2 b_2, then it becomes obvious:

\nabla \cdot \nabla = \frac{\partial}{\partial x} \left( \frac{\partial}{\partial x} \right) + \frac{\partial}{\partial y} \left( \frac{\partial}{\partial y} \right)

From there, the reason why it gives the second derivative is obvious.

 

[ameeno97]

Shouldn't the answer be first derivative squared !? \left(\frac{\partial}{\partial x}\right)^{2}

 

[Char. Limit]

Shouldn't the answer be first derivative squared !? \left(\frac{\partial}{\partial x}\right)^{2}

No, why would it be?

 

[ameeno97]

From above definition this just a dot product so just need to multiply
∂∂x i by ∂∂x i


isn't that we do when we take dot product of two vectors;multiplication !?

 

[I like Serena]

Isn't that the same thing?
$$\left({\partial \over \partial x}\right)^2 = {\partial \over \partial x} \cdot {\partial \over \partial x} = {\partial^2 \over \partial x^2}$$
I have to admit that this is not immediately clear intuitively, but it's true nonetheless.

As opposed to:
$$\left({\partial f \over \partial x}\right)^2 = {\partial f \over \partial x} \cdot {\partial f \over \partial x} \ne {\partial^2 f \over \partial x^2}$$

 

[ameeno97]

Isn't that the same thing?
$$\left({\partial \over \partial x}\right)^2 = {\partial \over \partial x} \cdot {\partial \over \partial x} = {\partial^2 \over \partial x^2}$$

Are you sure ?, from where have you brought this !? Could you proof that?

If that is true so what does that mean? How could multiplication results in the second derivative !?

regards

 

[I like Serena]

It's not really something to prove. It's a notational matter.

The notation ${\partial \over \partial x}$ represents an operator.
It needs to operate on a function to have meaning, in which case it's the derivative of the function.

Intuitively the $\partial$ is the "change" in something that comes after, which is divided by the change in x.
If these changes are small enough the result approximates the derivative.

In this context the multiplication is not really a multiplication, but it's an operator appliance, which behaves in most ways similar to a multiplication.
Since they are so similar, they are often denoted the same, although you should always be aware that you're talking about differentation, which does behave differently from multiplication sometimes.

from where have you brought this !?

It's part of how the Leibniz notation for derivatives works:
http://en.wikipedia.org/wiki/Leibniz's_notation

 

[Char. Limit]

I think the real problem here is the abuse of notation. Formally, you really shouldn't SAY that the gradient operator, as is, even exists on its own. It needs to be paired with a function, f, to exist. However, we allow this abuse of notation because it makes descriptions for things like the divergence and the curl much easier.