Laplace-Runge-Lenz vector problem

[wantommy]

The vector A is defined as the quantum version of the Laplace-Runge-Lenz vector,

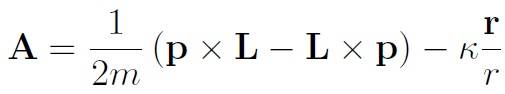
where

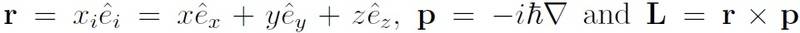
The system Hamiltonian is given by

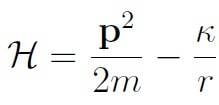
Show that

------------------------------------------------------------------

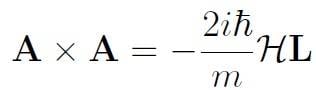
this problem confuse me for at least 2 years...
i can't derive it

Can any expert help me?
hope someone can write down specific derivation

Thanks a lot!

 

[mathman]

Mathematician's reply: Let X be any vector XxX = 0 (vector).

 

[Bill_K]

this problem confuse me for at least 2 years...
i can't derive it

wantommy, This is an excellent exercise. Even if you can find a complete solution on the web, I encourage you to work it out for yourself. I know of no shortcut, but with a systematic approach it shouldn't take you two years!

Hints: First of all, ditch the cross product notation and write out the components. This problem is about commutators, and the cross product obscures the factor ordering. For example, what you want to show is really

[A_i, A_j] = - 2iħ/m H ε_ijk L_k

Second, build the result up a piece at a time. Start with the commutators that are obvious:

[x_i, x_j] = 0
[p_i, p_j] = 0
[p_i, x_j] = iħ δ_ij

and most importantly,

[L_i, V_j] = - i ε_ijk V_k

where V is any vector operator.

Collect intermediate results like [p_i, L_j], [x_i, L_j] and [A_i, L_j].

Whoops, were you paying attention? You don't even have to work these out! They're all instances of [L_i, V_j].

Finally, make use of well-known identities like

ε_ijk ε_klm = δ_il δ_jm - δ_im δ_jl and

[A, BC] = [A,B] C + B [A,C]

Learning how to do a calculation systematically (and learning how to get it right!) is an important part of a physics education.