- 1,100
- 1,387
I haven't learned about Lie Groups yet, but came across this question.
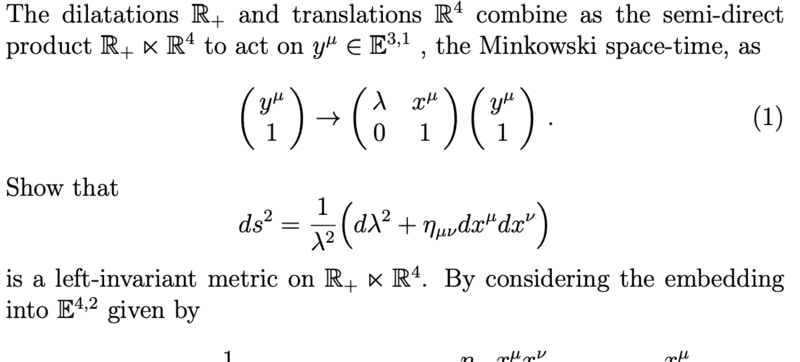
What I don't understand:
- is the semi-direct product ##R_+ \ltimes R^4## here a matrix group with elements ##\begin{pmatrix} \lambda & x^{\mu} \\ 0 & 1 \end{pmatrix}##? And is the group multiplication then matrix multiplication?
- I guessed that because ##R_+ \ltimes R^4 \sim R^5## that the metric acts on matrices ##g_1, g_2## in the group as it would acting on two vectors in ##R^5##, but what does it mean that the metric is left invariant? Is it that for an arbitrary matrix ##g_3## in the group that ##\langle g_1, g_2 \rangle = \langle g_3 g_1, g_3 g_2 \rangle##?
(Not sure if any of that's right and maybe it'd be better to actually learn the theory first, but sometimes a practical example can't hurt?)
What I don't understand:
- is the semi-direct product ##R_+ \ltimes R^4## here a matrix group with elements ##\begin{pmatrix} \lambda & x^{\mu} \\ 0 & 1 \end{pmatrix}##? And is the group multiplication then matrix multiplication?
- I guessed that because ##R_+ \ltimes R^4 \sim R^5## that the metric acts on matrices ##g_1, g_2## in the group as it would acting on two vectors in ##R^5##, but what does it mean that the metric is left invariant? Is it that for an arbitrary matrix ##g_3## in the group that ##\langle g_1, g_2 \rangle = \langle g_3 g_1, g_3 g_2 \rangle##?
(Not sure if any of that's right and maybe it'd be better to actually learn the theory first, but sometimes a practical example can't hurt?)