- #1
paralleltransport
- 128
- 97
- TL;DR
- I'd like to better understand the lehmann kallen representation of the propagator.
Hello,
My question pertains to the formula below:
In particular, I would like to ask about the spectral density function shown below:
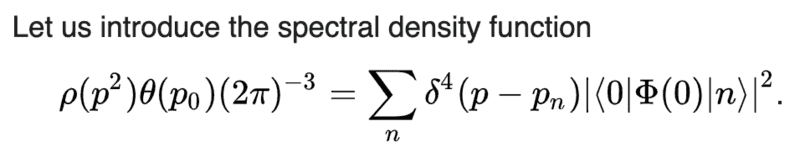What does the spectral function physically represent? Is there any interpretation of its meaning, whether it has a relation to the physical spectrum of the theory.
My work:
The propagator real poles correspond to particles (a particle is a lump of energy that doesn't decay or split), it seems to suggest that the spectral function would have delta functions at 1 particle state at rest. Obviously, in a lorentz invariant QFT, one can boost this one particle state to get a continuous spectrum, so \rho(p^2) is not the spectrum of the theory, but it has some relation to it.
Thank you.
My question pertains to the formula below:
In particular, I would like to ask about the spectral density function shown below:
My work:
The propagator real poles correspond to particles (a particle is a lump of energy that doesn't decay or split), it seems to suggest that the spectral function would have delta functions at 1 particle state at rest. Obviously, in a lorentz invariant QFT, one can boost this one particle state to get a continuous spectrum, so \rho(p^2) is not the spectrum of the theory, but it has some relation to it.
Thank you.