Leithold Calculus: Overcoming Difficulties & Learning Property

[dumplump]

I have recently purchased this textbook. When I compare it to my class, I find that the exercises are of significantly higher difficulty. There are tricks to solving the problems that I never would have thought of because quite honestly I never learned them. For example the textbook, chapter on integration by parts, there is a problem that is solved by adding and subtracting 1 from the numerator.

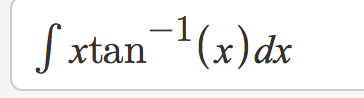
I did not know I could do that, and I was stuck until I plugged the problem into Symbolab.

Here is the property that is needed in order to solve, but I was not able to find the name of this property

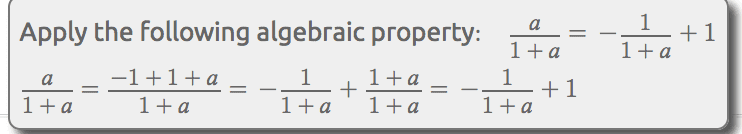
For those who have used this book, The Calculus 7 Louis Leithold, how did you overcome these difficulties? I have purchased Leithold's Before Calculus text as well. I feel that my previous textbook just was not sufficient because I did not see the following property above in the text, or should I say I do not remember it being in the text.

 

[Greg Bernhardt]

Thanks for the post! Sorry you aren't generating responses at the moment. Do you have any further information, come to any new conclusions or is it possible to reword the post?

 

[dumplump]

My post was mostly about how to overcome the difficulties presented in the text. It appears that this text is not used that much or no one has used it, and thus no responses.

 

[vanhees71]

Well, the problem is quite clear. The thread should be moved to the homework section. I guess you mean \tan^{-1} x=\arctan x. The notation \tan^{-1} for the inverse of a function is very bad. Never ever use it! It could be mistaken as \tan^{-1} x=1/\tan x.

Anyway, we want to solve
F(x)=\int \mathrm{d} x x \arctan x.
You can simplify this integral first by using integration by parts
\int \mathrm{d} x u'(x) v(x)=u(x) v(x)-\int \mathrm{d} x u(x) v'(x).
Setting u'(x)=x, v(x)=\arctan x. Then u(x)=x^2/2, v(x)=1/(1+x^2), leading to
F(x)=\frac{x^2}{2} \arctan x-\frac{1}{2} \int \mathrm{d} x \frac{x^2}{1+x^2}.
Now comes the simple trick
F(x)=\frac{x^2}{2} \arctan x - \frac{1}{2} \int \mathrm{d} x \frac{x^2+1-1}{1+x^2}= \frac{x^2}{2} \arctan x - \frac{1}{2} \int \mathrm{d} x \left (1- \frac{1}{1+x^2} \right )=\frac{x^2}{2} \arctan x -\frac{x}{2}+\frac{1}{2}\arctan x+C=\frac{x^2+1}{2} \arctan x-\frac{x}{2}+C.
To check this take the derivative again
F'(x)=x \arctan x + \frac{x^2+1}{2(x^2+1)}-\frac{1}{2}=x \arctan x.
:-).

 

[dumplump]

Well, the problem is quite clear. The thread should be moved to the homework section. I guess you mean \tan^{-1} x=\arctan x. The notation \tan^{-1} for the inverse of a function is very bad. Never ever use it! It could be mistaken as \tan^{-1} x=1/\tan x.

Anyway, we want to solve
F(x)=\int \mathrm{d} x x \arctan x.
You can simplify this integral first by using integration by parts
\int \mathrm{d} x u'(x) v(x)=u(x) v(x)-\int \mathrm{d} x u(x) v'(x).
Setting u'(x)=x, v(x)=\arctan x. Then u(x)=x^2/2, v(x)=1/(1+x^2), leading to
F(x)=\frac{x^2}{2} \arctan x-\frac{1}{2} \int \mathrm{d} x \frac{x^2}{1+x^2}.
Now comes the simple trick
F(x)=\frac{x^2}{2} \arctan x - \frac{1}{2} \int \mathrm{d} x \frac{x^2+1-1}{1+x^2}= \frac{x^2}{2} \arctan x - \frac{1}{2} \int \mathrm{d} x \left (1- \frac{1}{1+x^2} \right )=\frac{x^2}{2} \arctan x -\frac{x}{2}+\frac{1}{2}\arctan x+C=\frac{x^2+1}{2} \arctan x-\frac{x}{2}+C.
To check this take the derivative again
F'(x)=x \arctan x + \frac{x^2+1}{2(x^2+1)}-\frac{1}{2}=x \arctan x.
:).

The problem is clear, but that was not the premise of my question. The question was basically asks for people who have used this text, and how they overcame the difficulties of the text. No once did I state that I needed help solving the problem.

 

[George Jones]

The first-year calculus course that I took as a student many, many years ago used an earlier edition of Leithold as its text. I don't remember "problems" with it, but this could be due to the long passage of time.

Two important tricks are creatively adding zero or multiplying by one. It is sometimes useful to make a part of a numerator equal to the denominator. In this case, this was done by adding zero in the form $0 = -1 + 1$.

$$\frac{a}{1 + a} = \frac{-1 +1 +a}{1 + a} = \frac{-1}{1 + a} + \frac{1 + a}{1 + a}.$$

 

[dumplump]

The first-year calculus course that I took as a student many, many years ago used an earlier edition of Leithold as its text. I don't remember "problems" with it, but this could be due to the long passage of time.

Two important tricks are creatively adding zero or multiplying by one. It is sometimes useful to make a part of a numerator equal to the denominator. In this case, this was done by adding zero in the form $0 = -1 + 1$.

$$\frac{a}{1 + a} = \frac{-1 +1 +a}{1 + a} = \frac{-1}{1 + a} + \frac{1 + a}{1 + a}.$$

Thank you for pointing that out. I will keep an eye for it. That was the type of response I was looking for.

 

[dumplump]

Probably the most difficult textbook problem was trying to find the integral of xsin^-1(x) from 0 to 1 only using integration by parts. I had to confer with my TA, and specifically state that I needed to use integration by parts not trig substitutions.

 

[nearlynothing]

I used this text during my first three semesters at university for my calculus classes. It seems that the author aims at computational proficiency, basically what we did was learn the theory and then solve a whole lot of problems in class atthe same time as the teacher did it on the blackboard, that way you could always look if you got stuck. Besides that, we got assignments with a lot of problems to solvre on a regular basis.
If your class isn't like this maybe you should consider trying to solve as many problems as you can on your own.
On the other hand, tricks like the one you tslk about in the OP are seldom taught by themselves, you rather learn them when you get stuck and look for help like you did here, or maybe one day youre more creativethan usual and just come up with them yourself.
Anyways, the key is to tackle the problems and get the experience :)

 

[dumplump]

I used this text during my first three semesters at university for my calculus classes. It seems that the author aims at computational proficiency, basically what we did was learn the theory and then solve a whole lot of problems in class atthe same time as the teacher did it on the blackboard, that way you could always look if you got stuck. Besides that, we got assignments with a lot of problems to solvre on a regular basis.
If your class isn't like this maybe you should consider trying to solve as many problems as you can on your own.
On the other hand, tricks like the one you tslk about in the OP are seldom taught by themselves, you rather learn them when you get stuck and look for help like you did here, or maybe one day youre more creativethan usual and just come up with them yourself.
Anyways, the key is to tackle the problems and get the experience :)

Thanks for the reply. I acquired this book because I felt that in my current calculus 2 textbook has problems that are too simple. I just experienced the difficulty of Liethold's text, and thought I would reach out and ask those who have used the text to figure out how they overcame some of the difficulties of solving the problems. One problem that I was stuck on for quite sometime was integration by parts of xsin^-1(x). I had to refer to my TA in order to solve that problem.