Dophs
- 1
- 0
Hello so I'm a high school student and I came up with this question and I wanted to know if this was possible to do?
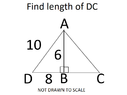
View attachment 8044
So I tried to research and find a way to find the length of DC and I couldn't find anything, so I am here to ask for help, is this possible? I figured it would go in the trigonometry section, if not please tell me what sub-forum is belongs in.
So obviously I know the left, right triangle is a 30,60,90 and the height of the right, right triangle is 6 and obviously it has a 90 degree angle. I couldn't think of anyway to get any further due to the not drawn to scale part due to . BC could be 100, 4, 67, 21, so the angles would change of that triangle, but 6 is the height of both.
View attachment 8044
So I tried to research and find a way to find the length of DC and I couldn't find anything, so I am here to ask for help, is this possible? I figured it would go in the trigonometry section, if not please tell me what sub-forum is belongs in.
So obviously I know the left, right triangle is a 30,60,90 and the height of the right, right triangle is 6 and obviously it has a 90 degree angle. I couldn't think of anyway to get any further due to the not drawn to scale part due to . BC could be 100, 4, 67, 21, so the angles would change of that triangle, but 6 is the height of both.