- #1
road_king
- 18
- 0
Linearization of Lagrange EOMs of an Inverted Pendulum
Hi Folks,
I am modelling a state space model of an Inverted Pendulum mounted on a cart over a balancing seesaw.
I developed the equations of motion using the Lagrangian approach an obtained 3 PDEs. I solved them using Mathematica 8 for the second order derivatives of the generalized coordinates, and using one of the new Mathematica functions obtained a linearized representation of the system. The model seems to me to be pretty convincing, but not for my Thesis director, who ask me to obtain a linearized model by myself
I try to use Mathematica to calculate the second order Taylor series expansion of the equations of movement but it only takes as variables the first two coordinates instead of the four that appeared in the equation.
Iif anyone may give me any idea it will be very appreciated.
First I defined the first equation of movement as a function of the 3 generalized coordinates [x[t], θ[t],α[t]] and vm[t], which is the voltage applied to the servo-motor. This 3 coordinates represent the position of the cart along the rack over the seesaw, the rotation of the seesaw around his fulcrum, and the rotation of the pendulum around the cart.
I believe I am using the correct syntax for that as I read in the program help...
Series[ expr, var1, var2, ... ]
Any suggestions of how to do the work?
Thank in advance!
Edit: I attach a pdf file with the mathematica code, the text is in Spanish but I think it is easyly readable. I will ask in the Mathematica subforum later, the expecific question with Series function. Excuse my bad English, please.The expressions I am asking for are on page 5.
I am sorry I have not any drawing of the system, but it it like this image
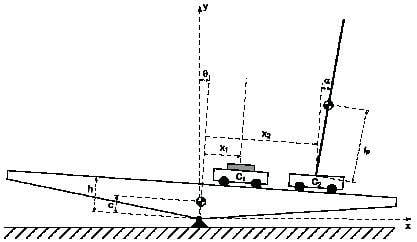
but without the c1 cart (my system only has one cart with the pendulum, and the names of the parameters and variables are different also)
Hi Folks,
I am modelling a state space model of an Inverted Pendulum mounted on a cart over a balancing seesaw.
I developed the equations of motion using the Lagrangian approach an obtained 3 PDEs. I solved them using Mathematica 8 for the second order derivatives of the generalized coordinates, and using one of the new Mathematica functions obtained a linearized representation of the system. The model seems to me to be pretty convincing, but not for my Thesis director, who ask me to obtain a linearized model by myself
I try to use Mathematica to calculate the second order Taylor series expansion of the equations of movement but it only takes as variables the first two coordinates instead of the four that appeared in the equation.
Iif anyone may give me any idea it will be very appreciated.
First I defined the first equation of movement as a function of the 3 generalized coordinates [x[t], θ[t],α[t]] and vm[t], which is the voltage applied to the servo-motor. This 3 coordinates represent the position of the cart along the rack over the seesaw, the rotation of the seesaw around his fulcrum, and the rotation of the pendulum around the cart.
I believe I am using the correct syntax for that as I read in the program help...
Series[ expr, var1, var2, ... ]
Any suggestions of how to do the work?
Thank in advance!
Edit: I attach a pdf file with the mathematica code, the text is in Spanish but I think it is easyly readable. I will ask in the Mathematica subforum later, the expecific question with Series function. Excuse my bad English, please.The expressions I am asking for are on page 5.
I am sorry I have not any drawing of the system, but it it like this image
but without the c1 cart (my system only has one cart with the pendulum, and the names of the parameters and variables are different also)
Last edited: