Lily's question at Yahoo Answers regarding kinematics

[MarkFL]

Here is the question:

AP physics/math question?

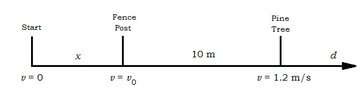
A mouse is moving with a constant acceleration along a straight ditch. It starts its stopwatch as it passes a fence post and notes that it takes it 10s to reach a pine tree 10m farther along the ditch. As it passes the pine tree, its speed is 1.2 m/s. How far was it from the fence post when it started from rest?

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Lily,

Let's first draw a diagram:

View attachment 1359

We may use the kinematics relations for constant acceleration:

\(\displaystyle \tag{1}v_f=at+v_i\)

\(\displaystyle \tag{2}v_f=\sqrt{2ad+v_i^2}\)

where:

\(\displaystyle v_f=\text{final velocity}\)

\(\displaystyle a=\text{acceleration}\)

\(\displaystyle d=\text{displacement}\)

\(\displaystyle v_i=\text{initial velocity}\)

Now, when the mouse starts, he begins from rest so his velocity is \(\displaystyle 0\frac{\text{m}}{\text{s}}\),when the mouse passes the fence post, his velocity is $v_0$, and when he passes the pine tree, his velocity is \(\displaystyle 1.2\frac{\text{m}}{\text{s}}\).

We also know that average velocity is displacement per time:

\(\displaystyle \overline{v}=\frac{d}{t}\)

For the interval between the fence post and the pine tree, we then find:

\(\displaystyle \overline{v}=\frac{10\text{m}}{10\text{s}}=1\frac{\text{m}}{\text{s}}\)

Since his velocity is increasing linearly, we know his instantaneous velocity in this interval at 5 seconds is equal to the average velocity, and so using (1), we may state:

\(\displaystyle 5a+v_0=1\)

And using (2), we have:

\(\displaystyle \frac{36}{25}=20a+v_0^2\)

Solving both equations for $a$, we then obtain:

\(\displaystyle a=\frac{1-v_0}{5}=\frac{36-25v_0^2}{500}\)

Which leads to the quadratic in $v_0$:

\(\displaystyle 25v_0^2-100v_0+64=0\)

Factoring, we find:

\(\displaystyle \left(5v_0-4 \right)\left(5v_0-16 \right)=0\)

Since we must have \(\displaystyle v_0<\frac{6}{5}\), we take the root:

\(\displaystyle v_0=\frac{4}{5}\frac{\text{m}}{\text{s}}\)

From this, we find from either of our two equations above:

\(\displaystyle a=\frac{1}{25}\frac{\text{m}}{\text{s}^2}\)

Now, on the interval between the start and the fence post, using (2) we find:

\(\displaystyle x=\frac{v_0^2}{2a}=\frac{ \left(\dfrac{4}{5}\dfrac{ \text{m}}{ \text{s}} \right)^2}{2\left(\dfrac{1}{25}\dfrac{ \text{m}}{ \text{s}^2} \right)}=8 \text{ m}\)