Linear systems: Tmax = Umax is not making sense

[LT72884]

Homework Statement

NA

Relevant Equations

delta(T+U)=0

We have a slide in class that states if no friction or damping force, then the system is conservative. Then it shows:

delta(T+U)=0 or T+U=constant. It then goes on to say that max kinetic energy is equal to max potential energy which is false.

no way can you have KEmax=Pemax... I double checked the slide and the book, and both say the same thing. Tmax=Umax.

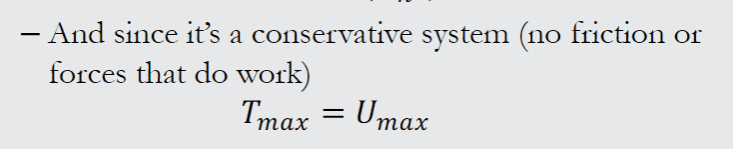
T is KE and U is PE. From every physics, dynamics, fluids, and statics course i have taken, when KE is max, PE is min. As a ball bounces or a spring bounces, at the bottom, velocity is high, and height is low. Holding a ball in my hand 3 feet from the ground, it has max PE, but no velocity so KE is min. If i drop the ball, near the bottom, velocity is high and the height of the ball is low.

thanks. Need some help understanding where they are coming from with this approach. even this simple website agrees with me:

https://www.ux1.eiu.edu/~cfadd/1150/06WrkEng/EngConsrv.html

 

[Orodruin]

It is not saying that max kinetic energy is obtained at the same time as max potential energy. It is saying that the max kinetic energy (obtained at the same time as the lowest potential) is the same as the max potential (obtained when kinetic energy is zero).

However, this is still false in general as potential energy depends on where you put your reference level. It is true only if you put the reference level at the lowest point of the potential.

 

[LT72884]

It is not saying that max kinetic energy is obtained at the same time as max potential energy. It is saying that the max kinetic energy (obtained at the same time as the lowest potential) is the same as the max potential (obtained when kinetic energy is zero).

However, this is still false in general as potential energy depends on where you put your reference level. It is true only if you put the reference level at the lowest point of the potential.

still does not make sense because now, after finding the equation of motion for my spring system, the example tells me to set 1/2mx`^2=1/2kx^2. these two are not equal to me, at all.

thanks

 

[PeroK]

Gravitational PE is often expressed as $U = -\frac{GMm}{r}$, which gives $U_{max} = 0$.

Personally, I wouldn't waste any time worrying about what the authors had in mind.

 

[Steve4Physics]

still does not make sense because now, after finding the equation of motion for my spring system, the example tells me to set 1/2mx`^2=1/2kx^2. these two are not equal to me, at all.

It sounds like you are analysing a mass oscillating on a horizontal spring (which you hadn't mentioned previously).

$T_{max}$ is attained when the mass passes through the equilibrium position. At that moment $T=T_{max}=E_{total}$.

$U_{max}$ is attained when the mass is at maximum displacement. At that moment $U=U_{max}=E_{total}$.

$T_{max}$ and $U_{max}$ are equal values. $T=T_{max}$ and $U=U_{max}$ at different times, as explained by @Orodruin.

There are four points in each cycle where $\frac 1 2 m\dot x^2=\frac 1 2kx^2$ (where kinetic and elastic potential energies are equal). At these points
$T=U = \frac {E_{total}}{2}$.

Minor edits.