Local truncation error from Taylor/Variable timestep

[maistral]

I am not sure where I should be posting this; I am perfectly aware this is Taylor expansion calculus, but considering the fact that I am working with numerical ODE solutions, I posted this here.

In the paper: Implementation of an Adaptive BDF2 Formula and Comparison with the MATLAB Ode15s (Celaya, et al); I have found this formula:

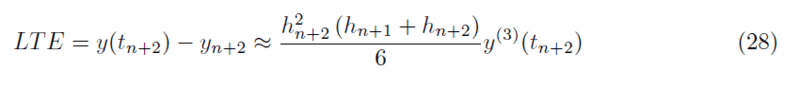
It's supposed to be a local truncation error formula which compares the numerical solution y_n+2 to that of a Taylor expansion y(t_n+2). While I can set the values of h to be equal with each other (thus retrieving the constant step version), I have no idea how to derive this term if I want to bring it to higher orders (say, I want a fourth-order solution which would den require the calculation of a fifth derivative term with variable stepsize).

TLDR: Does anyone know how this thing has been made? I have been scouring the internet for a while about this and I seem to have no information as to how this thing appeared (I mean, looking at the four papers I have now, this just magically appeared).

Thanks!

 

[pasmith]

Link to the full paper: https://www.researchgate.net/publication/275067432_Implementation_of_an_adaptive_BDF2_formula_and_comparison_with_the_MATLAB_Ode15s

I found https://student.cs.uwaterloo.ca/~cs370/notes/LTE.pdf which explain how to calculate LTEs and give the forwards Euler and Crank-Nicholson as examples.

Thus your starting point is the advancing formula (27) in which you set $y_{n+1} = y(t_{n+1})$, $y_n = y(t_n)$ and $f_{n+2} = y'(t_{n+2})$. The result you are looking for gives the error in terms of $y^{(3)}(t_{n+2})$, so you will then need to use these Taylor expansions: $$\begin{align*} y(t_{n+1}) &= \sum_{k=0}^\infty \frac{(t_{n+1} - t_{n+2})^k}{k!} y^{(k)}(t_{n+2}) \\ y(t_n) &= \sum_{k=0}^\infty \frac{(t_{n} - t_{n+2})^k}{k!} y^{(k)}(t_{n+2}) \end{align*}$$ I will say that starting from the constant-step version (26) I obtained $$y_{n+2} - y(t_{n+2}) = \frac 29 h^3y^{(3)}(t_{n+2}) + O(h^4)$$ so either I have gone astray or the paper contains an error.

 

[maistral]

Link to the full paper: https://www.researchgate.net/publication/275067432_Implementation_of_an_adaptive_BDF2_formula_and_comparison_with_the_MATLAB_Ode15s

I found https://student.cs.uwaterloo.ca/~cs370/notes/LTE.pdf which explain how to calculate LTEs and give the forwards Euler and Crank-Nicholson as examples.

Thus your starting point is the advancing formula (27) in which you set $y_{n+1} = y(t_{n+1})$, $y_n = y(t_n)$ and $f_{n+2} = y'(t_{n+2})$. The result you are looking for gives the error in terms of $y^{(3)}(t_{n+2})$, so you will then need to use these Taylor expansions: $$\begin{align*} y(t_{n+1}) &= \sum_{k=0}^\infty \frac{(t_{n+1} - t_{n+2})^k}{k!} y^{(k)}(t_{n+2}) \\ y(t_n) &= \sum_{k=0}^\infty \frac{(t_{n} - t_{n+2})^k}{k!} y^{(k)}(t_{n+2}) \end{align*}$$ I will say that starting from the constant-step version (26) I obtained $$y_{n+2} - y(t_{n+2}) = \frac 29 h^3y^{(3)}(t_{n+2}) + O(h^4)$$ so either I have gone astray or the paper contains an error.

Thanks for replying.

Actually I also have the same result as yours. I seem to be unable to replicate the constant step case. I, however, found this paper: Automatic selection of the initial step size for an ODE solver and taking a glance at Equation (3.3);

It's weird since it actually replicates the order of the formula of the first paper if I assign the constant step case! The coefficient is not the same however, the original one would result to something like 1/3 and this one would result to 1/6. Strange. At least your attempt also ends up with the same order of h, but all these varying constants confuse me even more

Anyway, I understand that the Taylor approach is quite straightforward. I am more curious however how the varying stepsize formulation is obtained. Could this be actually related to Lagrange polynomials? As far as I understand the only means for one to extract variable-step BDF formulations is via a polynomial interpolation approach.