- #1
dynamicskillingme
- 27
- 0
Homework Statement
Has solution
It then goes on to state the solution blows up at
My issue is when I do the solution I get
(Working)
dynamicskillingme said:[itex] \dot{y} = y^2 [/itex]
[itex] y = yt + c [/itex] ; for [itex] t = 0 [/itex]
dynamicskillingme said:Homework Statement
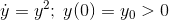
Has solution
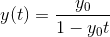
It then goes on to state the solution blows up at, which I understand.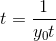
My issue is when I do the solution I get
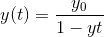
(Working)
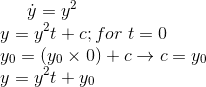
dynamicskillingme said:How could I prove their answer, or what should I read up on to be able to show this proof?
A simple Lipshitz condition is a mathematical concept that is used to ensure the stability of a system. It states that the rate at which a function changes should not exceed a certain bound, known as the Lipschitz constant, for any two points in the system.
The Lipschitz condition is important because it guarantees the stability of a system. If a system satisfies the Lipschitz condition, it means that even small changes in the input will result in small changes in the output, ensuring that the system behaves predictably and reliably.
The Lipschitz condition is used in various fields such as control theory, differential equations, and optimization. It is particularly useful in the study of dynamical systems, which are systems that change over time. For example, the Lipschitz condition can be used to analyze the stability of a chemical reaction or the predictability of weather patterns.
To determine if a system satisfies the Lipschitz condition, you need to calculate the Lipschitz constant. This is done by finding the maximum rate of change of the function over a given interval. If this rate of change is less than or equal to the Lipschitz constant, then the system satisfies the Lipschitz condition.
No, the Lipschitz condition is not always satisfied. It depends on the specific system and the function being analyzed. In some cases, it may be necessary to modify the system or the function to ensure that the Lipschitz condition is satisfied.