Magnetic field from a square loop

[Potatochip911]

Homework Statement

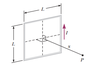
A wire is formed into the shape of a square of edge length L. Show that when the current in
the loop is I, the magnetic field at point P a distance x from the center of the square along its axis is $$B=\frac{\mu_0 IL^2}{2\pi(x^2+L^2/4)\sqrt{x^2+L^2/2}}$$

Homework Equations

$d\vec{B}=\frac{\mu_0}{4\pi}\frac{I\vec{ds}\times\hat{r}}{r^2}$

The Attempt at a Solution

[/B]
$d\vec{B}=\frac{\mu_0}{4\pi}\frac{I\vec{ds}\sin\theta}{r^2}$ where $\theta$ is the angle between $\hat{r}$ and $\vec{ds}$ therefore $\sin\theta=\sqrt{\frac{x^2+L^2/4}{z^2+x^2+L^2/4}}$
From the symmetry of the problem it's clear that only the components parallel to $x$ will be leftover which seem to be given by $\sin\phi$ but in the solution they are given by $\cos\phi$ which doesn't make any sense to me.

 

[TSny]

What angle does $d\vec{B}$ make to the x axis?

 

[Potatochip911]

What angle does $d\vec{B}$ make to the x axis?

Okay I got the angle it makes with the x-axis from the most basic case where $x=0$

On one side of the x-axis all angles must add up to $\pi$ therefore (where x is the angle between $d\vec{B}$ and the x axis):
$$
\pi=(\pi/2-\phi)+\pi/2+x\Longrightarrow x=\phi
$$

Thanks it makes sense now!

 

[TSny]

On one side of the x-axis all angles must add up to $\pi$ therefore (where x is the angle between $d\vec{B}$ and the x axis):
$$
\pi=(\pi/2-\phi)+\pi/2+x\Longrightarrow x=\phi
$$

Yes. Nice.