Magnetic Field of a Moving Point charge

[OmegaFury]

Homework Statement

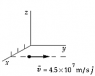
A point charge of q₁=3.6nC is moving with speed 4.5 x 10⁷m/s parallel to the y-axis along the line x=3m. The magnetic field produced by this charge at the origin when it is at the point x=3m, y=4m is approximately:

Homework Equations

vector B= (magnetic constant/4pi) (q(vector v X unit vector r)/r²)
magnetic constant= 4pi x 10^-7 (Tesla x meter)/Ampere

The Attempt at a Solution

The problem here is a curious cross product outcome.
vector v= 4.5 x 10⁷j = <0, 4.5 x 10⁷, 0>
vector r= <3-0, 4-0, 0-0>= <3,4,0>
magnitude of r= sqrt(3²+4²)= 5
unit vector r= vector r/ magnitude of vector r= <3,4,0>/5

$\vec{v}$X$\hat{r}$= <0, 4.5 x 10⁷, 0> X <3, 4, 0> =

((4.5 x 10⁷(0) - 0(4))i - (0(0) - 0(3))j + (0(4) - 4.5 x 10⁷(3))k)/5 =

(-13.5 x 10⁷j)/5= <0, 0, -13.5 x 10⁷>/5

Wouldn't that imply that the cross product vector is in the -Z direction? However, using right hand rules, shouldn't the cross product vector be in the positive Z direction?

 

[Redbelly98]

Welcome to PF.

In the Biot Savart Law, the direction of r is from the current element or charge to the point where B is being calculated. So r is <-3,-4,0> in this case.

p.s. I presume the charge is moving in the +y direction?

 

[OmegaFury]

Welcome to PF.

In the Biot Savart Law, the direction of r is from the current element or charge to the point where B is being calculated. So r is <-3,-4,0> in this case.

Ahhhhh. So I had it reversed.

p.s. I presume the charge is moving in the +y direction?

Yes, the charge is moving in the +y direction.

So the cross product would now be: <0, 4.5 x 10⁷, 0>m/s X <-3, -4, 0>/5 =
(0--(3/5)(4.5 x 10⁷)) k= +2.7 x 10⁷m/s k

Then vector B= (magnetic constant/ 4pi) (3.6 x 10^-9C)(2.7 x 10⁷m/s k) / (25m²)= 3.89 x 10^-10 T k. Which is equal to 0.39nT k

Thank you for your assistance :)