Magnetic Forces on infinite current-carrying wires

[cookiemnstr510510]

Homework Statement

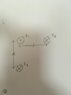
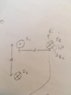
A) Three infinite, current-carrying wires are arranged as shown below. In terms of the given quantities, determine the magnitude and direction of the magnetic force per length acting upon wire 2. (Part A.jpg attached)
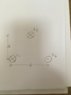
B) Three infinite, current-carrying wires are arranged as shown below in terms of the given quantities, determine the magnitude and direction of the magnetic force per length acting upon wire 5.(Part B.jpg attached)

Homework Equations

B=(μ₀I)/(2πd)
F=ILxB

The Attempt at a Solution

A) Both wires 1 and 3 create a magnetic field at the location of wire 2.
Wire 1's magnetic field points straight upward in the j-hat direction.
Wire 3's magnetic field points at a -45° angle from the positive i-hat direction which is from left to right.

Using right hand rule:

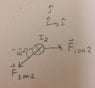
F_{1 on 2} is in the positive i-hat direction
and
F_{3 on 2} is -45° from the negative i-hat direction
These forces are shown in (forces.jpg)

F_1on2=I₂LB₁i-hat
B₁=(μ₀I₁)/(2πd)
therefore:
F_1on2=(I₂I₁LB₁)/(2πd) i-hat

F_{3 on 2}=I₂LxB₂= here is where I am stuck- when doing the cross product here is the θ the angle between both wires? I guess I am confusing the cross product we do for magnetic field and the one we do for forces..

Any help would be appreciated!

 

[kuruman]

The magnetic force directions you show are incorrect. The magnetic force due to each wire is not along the line joining the wires but perpendicular to it as prescribed by the right hand rule.

 

[cookiemnstr510510]

Hello kuruman!
So I was thinking about the magnetic field as (magneticfield.jpg) (Small error in my picture where it says B₂ it should say B₃)
From there I did the RHR and obtained my forces.
I guess I am still incorrect?

 

[kuruman]

The directions for the magnetic fields are correct as shown in post #3. Now you have to do another right hand rule diagram for the forces.

 

[cookiemnstr510510]

The directions for the magnetic fields are correct as shown in post #3. Now you have to do another right hand rule diagram for the forces.

Hmm, okay. So for B₁ for image in post 3, I point my four fingers in the direction of current of the wire in question (wire with current I2) and curl my fingers up towards B₁ which would result in a force directly to the right. Is this correct? or am i confusing RHR's
I can try to draw a picture of what I am representing if that would make it easier to understand.

 

[kuruman]

There are many ways to use one's fingers for the right hand rule. Please post a drawing of the two forces acting on the wire and we'll take it from there.

 

[cookiemnstr510510]

I guess I am not seeing how my Forces.jpg image is incorrect in post 1. I realize you said that the forces need to be perpendicular to the line adjoining wires, so does that mean into or out of the page since those are both perpendicular to the lines adjoining them?

 

[kuruman]

I guess I am not seeing how my Forces.jpg image is incorrect in post 1.

Sorry, your forces in that diagram are correct. I got confuse with the mislabeled B₂ that should have been a B₃. You now need to write F₃ in component form and add the two forces.

 

[cookiemnstr510510]

Sorry, your forces in that diagram are correct. I got confuse with the mislabeled B₂ that should have been a B₃. You now need to write F₃ in component form and add the two forces.

ahh, okay. Yes my images were confusing!

So I am getting the total force acting on wire 2 is:
From here on out F_{1 on 2}= F₁₂
and F_{3 on 2}=F₃₂

F_total=F₁₂(i-hat) - F₃₂cos(45°)(i-hat) - F₃₂sin(45°)(j-hat)

 

[cookiemnstr510510]

After thinking about a bit more:
F=ILxB
F₁₂=I1LB₁sin(90)(i-hat)=I1LB(i-hat)
The question is asking for Force per length so
(F₁₂/L)=I₁B₁(i-hat)
and
F₃₂=I₃LxB₃sin(90) (-cos(45)-sin(45)) I am saying sin(90) for the cross product because the angle between current I₂ and B₃₂ is 90 degrees... Therefore
F₃₂=-I₃LB[₃(√2)/2](i-hat) - I₃LB₃[(√2)/2](j-hat)
(F₃₂/L)=-[(√2)/2]I₃B₃(i-hat)-[(√2)/2]I₃B₃(j-hat)

(F_total/L)=I₁B₁(i-hat)-[(√2)/2]I₃B₃(i-hat)-[(√2)/2]I₃B₃(j-hat)