Mass attached to a rotating spring

[Santilopez10]

Homework Statement

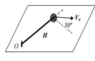
Figure shows a body of mass $m$ laying on a frictionless table and subdued to interaction with a elastic band of natural lenght H and constant k, which is fixed to the origin $O$. Suppose we give the object an initial velocity $V_0$ as shown in the image:
a) Obtain expressions for the transverse and radial components of the velocity vector as functions of the distance to O.
b) Suppose the radial component of the velocity is 0 at t=0. Find an expression for the maximum displacement of the elastic band.

Relevant Equations

.

a)
Our force can be represented as: $$\vec F= -k(r-H) \hat r$$ then the equations of motion are: $$\hat r: \ddot r -r {\dot{\theta}}^2=-\frac{k}{m_1}(r-H)$$ $$\hat{\theta}: r \ddot{\theta} + 2 \dot r \dot{\theta}=0$$
Plus we know that angular momentum is constant then $$|\vec L|=m r^2 \dot{\theta}$$
From the image we know that $\vec{V_0}=\frac{V_0}{2} \hat r - \frac{\sqrt{3}}{2} V_0 \hat{\theta}$ then at that instant $\dot r=\vec {V_0}_{\hat r}=\frac{V_0}{2}$ and $\dot{\theta}=-\frac{\sqrt{3}}{2H} V_0$ and we find the angular momentum of the system $$|\vec L|= \frac{\sqrt{3}}{2} m H V_0 = m r^2 \dot{\theta}$$
I have 3 equations for 4 unknowns, so I must be missing something. Plus, to be honest, I do not feel confortable with what I have done, I am not quite sure it is correct. Any help would be appreciated.

 

[haruspex]

a)
Our force can be represented as: $$\vec F= -k(r-H) \hat r$$

Not quite... it is an elastic band, not a spring.

The two equations of motion you posted, together with initial conditions, completely describe the system. The angular momentum equation is derivable from those, not additional.
Similarly, you could derive or assume conservation of energy.

 

[Santilopez10]

Not quite... it is an elastic band, not a spring.

The two equations of motion you posted, together with initial conditions, completely describe the system. The angular momentum equation is derivable from those, not additional.
Similarly, you could derive or assume conservation of energy.

Any tip on how to solve it? the system of diff equations seems too hard for my level to be honest.

 

[TSny]

See how far you can get with just conservation of angular momentum and energy.

 

[Santilopez10]

So I wrote $\dot{\theta}$ in terms of my angular moment to get: $$\dot{\theta}=-\frac{\sqrt{3}}{2} \frac{H V_0}{r^2}$$ and plugged it in the velocity equation in polar coordinates to get $$ \vec v= \dot r \hat r-\frac{\sqrt{3}}{2} \frac{H V_0}{r}\hat{\theta}$$ but I am still missing an expression for $\dot r$ as a function of r itself.

For b) I wrote the initial energy as $E_0=\frac{1}{2}m{V_0}^2$ then to find the maximum displacement I did: $$E_{max}=\frac{1}{2}k(r_{max}-H)^2=E_0 \rightarrow r_{max}=\sqrt{\frac{m}{k}}V_0+H$$
I do not know why they clarify that the initial radial component of velocity is 0 though, I did not need to take that into account to obtain my maximal displacement. Any help with finding $\dot r$ would be appreciated.

 

[TSny]

$$ \vec v= \dot r \hat r-\frac{\sqrt{3}}{2} \frac{H V_0}{r}\hat{\theta}$$

OK

but I am still missing an expression for $\dot r$ as a function of r itself.

Use the energy equation.

You'll need to think about what happens if r becomes less than H. As @haruspex noted, you are not dealing with a spring. You are dealing with a cord that can go slack.

For b) I wrote the initial energy as $E_0=\frac{1}{2}m{V_0}^2$ then to find the maximum displacement I did: $$E_{max}=\frac{1}{2}k(r_{max}-H)^2=E_0 \rightarrow r_{max}=\sqrt{\frac{m}{k}}V_0+H$$
I do not know why they clarify that the initial radial component of velocity is 0 though, I did not need to take that into account to obtain my maximal displacement. Any help with finding $\dot r$ would be appreciated.

You have assumed that there is no kinetic energy at maximum displacement. Is this true?

 

[Santilopez10]

OK
Use the energy equation.

You'll need to think about what happens if r becomes less than H. As @haruspex noted, you are not dealing with a spring. You are dealing with a cord that can go slack.

You have assumed that there is no kinetic energy at maximum displacement. Is this true?

Using the energy equation I got: $$r=\sqrt{\frac{m}{k}({V_0}^2-v^2)}+H \rightarrow \dot r= -\frac{\dot v v}{r-H}$$ Should I use this? it still has modulus of acceleration and velocity in its expression.

 

[Santilopez10]

Now I realize that in the expression of the energy, $\frac{1}{2}mv^2=\frac{1}{2}m({\dot r}^2+{r \dot{\theta}^2)}$ so then $$\frac{1}{2}m{V_0}^2=\frac{1}{2}m({\dot r}^2+{r \dot{\theta}^2)}+\frac{1}{2}k(r-H)^2$$ and substituing our already known expression of $\dot{\theta}$ we can Isolate for the variable $\dot r$. Is this correct?

 

[haruspex]

Now I realize that in the expression of the energy, $\frac{1}{2}mv^2=\frac{1}{2}m({\dot r}^2+{r \dot{\theta}^2)}$ so then $$\frac{1}{2}m{V_0}^2=\frac{1}{2}m({\dot r}^2+{r \dot{\theta}^2)}+\frac{1}{2}k(r-H)^2$$ and substituing our already known expression of $\dot{\theta}$ we can Isolate for the variable $\dot r$. Is this correct?

You need some more parentheses in there.

 

[Santilopez10]

You need some more parentheses in there.

you mean writing it like this? $$
\frac{1}{2}m{V_0}^2=\frac{1}{2}m(({\dot r})^2+{r (\dot{\theta})^2)}+\frac{1}{2}k(r-H)^2$$

 

[haruspex]

you mean writing it like this? $$
\frac{1}{2}m{V_0}^2=\frac{1}{2}m(({\dot r})^2+{r (\dot{\theta})^2)}+\frac{1}{2}k(r-H)^2$$

That didn't change anything, only made the error clearer. Check the dimensions of the terms. Are they consistent?

 

[Santilopez10]

That didn't change anything, only made the error clearer. Check the dimensions of the terms. Are they consistent?

oh my bad. $$
\frac{1}{2}m{V_0}^2=\frac{1}{2}m({\dot r}^2+{(r \dot{\theta})^2)}+\frac{1}{2}k(r-H)^2$$

 

[haruspex]

oh my bad. $$
\frac{1}{2}m{V_0}^2=\frac{1}{2}m({\dot r}^2+{(r \dot{\theta})^2)}+\frac{1}{2}k(r-H)^2$$

Right.

 

[Santilopez10]

Right.

Okay but I am still missing the second answer. I tried to use conservation of linear momentum and energy but I got a ciclyc answer. Any tips on how should I approach it?

 

[haruspex]

Okay but I am still missing the second answer. I tried to use conservation of linear momentum and energy but I got a ciclyc answer. Any tips on how should I approach it?

You are asked for a maximum r. Why is a cyclic trajectory a problem? For the interval from t=0 to the first maximum displacement the elastic remains taut, so can be treated as a spring.
Are you concerned that a greater maximum could be reached later, after the elastic has passed through a slack phase? If so, I don't think you are supposed to worry about that.

Please post what you have.

Edit: Did you mean you get a quartic to solve for the answer? I do.

 

[Santilopez10]

You are asked for a maximum r. Why is a cyclic trajectory a problem? For the interval from t=0 to the first maximum displacement the elastic remains taut, so can be treated as a spring.
Are you concerned that a greater maximum could be reached later, after the elastic has passed through a slack phase? If so, I don't think you are supposed to worry about that.

Please post what you have.

By cyclic answer I meant this:
first we know that the initial velocity is only in the transverse direction so $\vec v_0= V_0 \hat{\theta} \rightarrow \dot{\theta}_0= \frac{V_0}{H}$ and from angular momentum we get $\dot{\theta}=\frac{H V_0}{r^2}$.
Second, using linear momentum conservation: $$m V_0=m(\sqrt{\dot r^2+ r^2 {\dot{\theta}}^2}) \rightarrow \dot r^2= V_0^2(1-\frac{H^2}{r^2})$$ Pluggin them in the energy equation I get $$ [V_0^2(1-\frac{H^2}{r^2})+\frac{H^2 V_0^2}{r^2}]+\frac{k}{m}(r-H)=V_0^2$$ which after simplifying ends in $r=H$ which is what I meant by cyclic answer. I suppose I should find an equation for r as a function of something but all the methods I tried like writing motion equations end in really difficult diff equations.

 

[kuruman]

Second, using linear momentum conservation: ...

Why is linear momentum conserved? The body of mass $m$ is acted upon by the external force of the elastic band which is fixed at point O which is fixed on the Earth. Unless you consider as your system Earth + mass, because an external force is acting on the system, the linear momentum of the mass is not conserved. However the angular momentum of the mass is indeed conserved because the elastic band exerts no torque.

 

[Santilopez10]

Why is linear momentum conserved? The body of mass $m$ is acted upon by the external force of the elastic band which is fixed at point O which is fixed on the Earth. Unless you consider as your system Earth + mass, because an external force is acting on the system, the linear momentum of the mass is not conserved. However the angular momentum of the mass is indeed conserved because the elastic band exerts no torque.

Okay, I understand what you are saying. So what quantity should I use to find my answer?

 

[haruspex]

Okay, I understand what you are saying. So what quantity should I use to find my answer?

You are already using energy and angular momentum, and that radial velocity is zero at max displacement. That is enough.

 

[Santilopez10]

You are already using energy and angular momentum, and that radial velocity is zero at max displacement. That is enough.

OOOOH I did not think about radial velocity being 0 at max, you are right! thanks a lot.

 

[haruspex]

OOOOH I did not think about radial velocity being 0 at max, you are right! thanks a lot.

Hmm... yes... for some reason I thought you already used that. I should have just given a hint and let you work that out.