What Forces Act on a Mass Sliding Inside a Hoop?

[Becca93]

Homework Statement

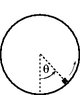
A mass M of 5.20E-1 kg slides inside a hoop of radius R=1.40 m with negligible friction. When M is at the top, it has a speed of 5.27 m/s. Calculate size of the force with which the M pushes on the hoop when M is at an angle of 27.0 degrees.

Picture attached at the bottom.


The attempt at a solution

E at the top of the circle should equal the energy at that particular part of the circle. So,

mg(2r) + (1/2)mvtop2 = mg(r-rcosθ) + (1/2)mv^2
m's cancel, so
g(2r) + (1/2)vtop2 = g(r-rcosθ) + (1/2)v^2
2(g(2r) + (1/2)vtop2 - g(r-rcosθ) = v^2

a = v^2/r

F = ma


When I plug everything in, I get
2(39.831) = v^2
v^2 = 79.66

a = 79.66/1.4
a = 56.90

F = (.52)(56.90)
F = 29.59 N

This answer is incorrect.

Please, can someone let me know where I'm going wrong?

 

[gneill]

You've calculated the force due to the circular motion, but what other force is also working on the mass?

 

[Becca93]

You've calculated the force due to the circular motion, but what other force is also working on the mass?

Okay. I'm forgetting the force of gravity acting on the mass, aren't I?

Should I add mgcosθ to my answer? Is that all I'm missing?

 

[gneill]

Okay. I'm forgetting the force of gravity acting on the mass, aren't I?

Should I add mgcosθ to my answer? Is that all I'm missing?

That looks right. Since the hoop has "negligible friction", only the component of the force due to gravity that is normal to the hoop's surface should matter -- the other component acts to accelerate the mass tangentially.

 

[asteriatic]

I would like to first commend your attempt at solving this problem. However, I believe there may be a mistake in your calculations.

Firstly, I would like to clarify that the mass M is not sliding on a horizontal surface, but rather on a circular path. Therefore, the equation for energy conservation should be:

mg(2r) + (1/2)mvtop^2 = mg(r-rcosθ) + (1/2)mv^2

Also, the value of v^2 that you have calculated is the total velocity at that point, and not the tangential velocity that is needed for calculating the force. The tangential velocity can be found by multiplying the total velocity by the sine of the angle, in this case, 27 degrees.

So the equation for acceleration would be:

a = vtan^2/r = (vtop sinθ)^2/r = (5.27 sin27)^2/1.4 = 2.44 m/s^2

Finally, the force can be calculated by multiplying the mass with the tangential acceleration:

F = ma = (0.52)(2.44) = 1.27 N

I hope this helps. Keep up the good work!