Mathematical Model for Convection Currents

[cdrake3]

I have a difficult problem on my research exploration for math. I am modeling the convection currents of boiling water in a pot, which is heated by an electric stove. There is a constant supply of energy at 8000 watts (the average for a stove) that heats the pot from the bottom of the pot, which has a circular base.
My Assignment: I have to create a 2-D mathematical model for a convection current in a cylinder object with heat source on bottom late – then demonstrating a slope field for the velocity of water as it rises. I have to solve for various velocities throughout the position of the pot. For example, I must generate an equation that models this phenomenon and a 2-D Graph (slope field) from it – looking something like this (just an example – the below is not the correct graph for the convection situation that I’m modeling):

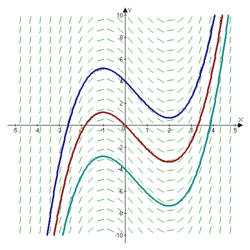Where I’m Stuck: Currently, I’m not quite sure of how I should go approaching this problem; specifically what is the right governing math equation (formula) for this situation:

• 2-D convection current
• Cylindrical shape
• Circular plate heat source underneath (8,000 watts)

In addition, I need to find the right formula that will create a model for a slope field – such that I can product a graph from it (to model convection velocities).

I have some research done below – but I’m not finding the right-fit formula to address my problem. There seems to be several physics and mathematical expressions that come together for the solution I seek – but I don’t know how exactly or if I am following the right approach. Here goes:

General Convection-Diffusion Equation:
The general equation is:

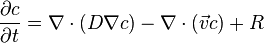
where
• c is the variable of interest (species concentration for mass transfer, temperature for heat transfer),
• D is the diffusivity (also called diffusion coefficient), such as mass diffusivity for particle motion or thermal diffusivity for heat transport,
• v is the average velocity that the quantity is moving. For example, in advection, c might be the concentration of salt in a river, and then would be the velocity of the water flow. As another example, c might be the concentration of small bubbles in a calm lake, and then would be the average velocity of bubbles rising towards the surface by buoyancy (see below).
• R describes "sources" or "sinks" of the quantity c. For example, for a chemical species, R>0 means that a chemical reaction is creating more of the species, and R<0 means that a chemical reaction is destroying the species. For heat transport, R>0 might occur if thermal energy is being generated by friction.
• ∇ represents gradient and represents divergence.

There is more information that I am using in the link below:
http://en.wikipedia.org/wiki/Convection–diffusion_equation#General

Where do I go from here?: from this point, I’m totally lost on if the above general equation is correct or not for my specific problem – and if it is, then how do I apply it?

Beyond that, I need to create a mathematical model for the slope field of convection current velocities – which is my ultimate aim for the overall assignment.

Can you help me to organize my approach from here?
How do I apply the general formula above? Considering that I have a 2-D cylinder problem and a 1-side heat source (bottom circle surface).
Do you have any guidance on slope field formulas/equations?

I thank you for your help in advance – I am hoping that you can help point me in the right direction.

 

[cdrake3]

People I know you have it in you. Someone out there must have at least some advice?

 

[Chestermiller]

You have only included one of the physical mechanisms for your problem. The mechanism you have included is the heat transport mechanism. The actual heat transfer equation is a little different from what you have written, but you have the right idea. What you are missing is the fluid mechanics equations, including buoyancy. When part of the liquid is heated, it expands, and this creates a buoyant force on it. This must be included in the Navier Stokes equations in order to calculate the velocity distribution. The velocity distribution and the temperature distribution are coupled with one another. So you need to solve the axisymmetric viscous flow equations simultaneously with the heat transfer equation. To formulate this problem, you need to learn some fluid mechanics and some convective heat transfer. What is going to be happening in your problem is that the fluid parcels are going to be moving upward at the center of the cylinder, and downward near the walls of the cylinder. The flow will turn around at the top and bottom. To learn more about all this, see Transport Phenomena by Bird, Stewart, and Lightfoot.

Chet

 

[Alkim]

Hi, I think you can use finite elements or finite difference to solve this. It reminds me electromagnetic problems where you have coupled differential equations (Maxwell equations) which you can solve numerically by finite elements or finite difference time domain methods. The following documents I found by a quick search might be helpful: http://www.tafsm.org/PUB_PRE/cALL/c34-ECM-MBI.pdf
http://en.wikipedia.org/wiki/Computational_fluid_dynamics