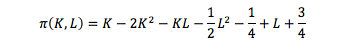SUMMARY
The discussion focuses on maximizing the profit function of two variables, K and L, represented by the equation $$\pi(K,L)=K-2K^2-KL-\frac{1}{2}L^2+L+\frac{1}{2}$$. Participants emphasize the importance of finding critical points by solving the first partial derivatives $$\pi_K(K,L)=0$$ and $$\pi_L(K,L)=0$$, followed by applying the second partials test for relative extrema. The conversation highlights the need for clarity in the profit function's formulation and encourages a step-by-step approach to differentiation.
PREREQUISITES
- Understanding of partial derivatives and their applications
- Familiarity with profit maximization concepts in economics
- Knowledge of the second partials test for relative extrema
- Basic algebra for manipulating equations
NEXT STEPS
- Study the method of finding critical points in multivariable functions
- Learn about the second partials test and its application in optimization
- Explore examples of profit maximization in economic models
- Review differentiation techniques for functions of multiple variables
USEFUL FOR
Students and professionals in economics, mathematicians, and anyone involved in optimization problems related to profit functions.