- #1
kshitij
- 218
- 27
- Homework Statement
- A test has 60 questions. Each question has 4 options with only one correct answer and their marking scheme is, +4 for correct response, 0 for no response and -1 for incorrect response. A student knows the correct answer to only 45 questions. What is the ideal number of guesses the student should make, such that the probability for the student to benefit/profit (i.e, score 180 or more marks) from these guesses is maximum?
- Relevant Equations
- Basic Probability Formulas
To approach this, I first assumed the case when the students attempts all the remaining questions.
Probability that they gain 4 marks for a guess = ##\frac 1 4##
Probability that they lose 1 for a guess = ##\frac 3 4##
Now let us say the number of correct guesses = ##r##
Now we should have at least 3 correct guesses,
because in this case they will score
45⋅4+3⋅4-12⋅1=180+0 marks
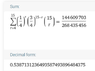
So our required probability = ## \sum_{r=3}^{15}\binom {15} r \frac 1 4^r \frac {3} {4}^{15-r}##
this gives us

So, there is approx 76% chance that they can benefit from attempting all the remaining questions.
Now, just to get a better idea of the situation, let's consider another scenario where the student knew the correct answers to 50 questions.
Here it might seem that if the student knew more,
then the risk of attempting rest of the questions should be lower.
For this is the case, our limiting value is 2 correct guesses as 2⋅4-8⋅1=0,

Surprisingly, here we have only 75% chance to benefit!
So, its actually less than the previous case. So, this definitely doesn't work as I thought it should.
For now, let's stick to our original question,
In the above cases I assumed that the student attempted all the questions which they couldn't solve,
but they don't necessarily have to, so my answer is incomplete.
Now, this question is not out of any textbook so I don't even know that whether this is a valid question,
Of course, even though I don't have an idea that which cases will have a higher probability, I can simply just do all the cases one by one, i.e., we can assume that they attempts all the questions and then find its probability of profit and then similarly we can do this by assuming that they attempted only 14 and then 13... and so on. And Finally we can compare out of all these cases which one has the highest probability of profit.
But I wanted a more generalized approach,
First, because this way we can extend this question to lots of other cases like, what happens when the student knew only 40 out of 60 questions?
We can still do the above process here, but there must be some way to form a function which could altogether give us the probability for all such possible cases.
Second reason is because what I actually want to know is how to maximize your marks in MCQs?
And to answer this question we will have to consider the marks scored by the student as well.
As in the original (made up) question, I only talked about "benefit/profit". Which means that even if the student scored 180 marks or 181 marks, this is considered as profit.
But that does not "maximize" the student's marks.
But again to answer such questions, one doesn't have a definite answer. All we can have is probabilities. This becomes a much harder problem.
So, in the end, I believe that if we could answer the simpler problem (the one in the homework statement), and we could generalize this situation, then maybe we could have a better idea on how to maximize our marks by comparing the situations, this time by taking both the marks scored in a case and the probability to score that marks in that case, into account simultaneously.
This way we could finally say that, yes, even though the probability to "X" marks is low, but the profit here is so high that it should be the best situation!
P.S., I know that the case when the student scores 180 marks is not actually a profit, but I considered this as benefit/profit because if the student doesn't lose marks, they can take this risk and attempt even the questions they couldn't solve. Its a win-win situation for them.
Edit: The question should also include that at least one guess is made by the student.
Probability that they gain 4 marks for a guess = ##\frac 1 4##
Probability that they lose 1 for a guess = ##\frac 3 4##
Now let us say the number of correct guesses = ##r##
Now we should have at least 3 correct guesses,
because in this case they will score
45⋅4+3⋅4-12⋅1=180+0 marks
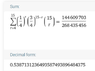
So our required probability = ## \sum_{r=3}^{15}\binom {15} r \frac 1 4^r \frac {3} {4}^{15-r}##
this gives us
So, there is approx 76% chance that they can benefit from attempting all the remaining questions.
Now, just to get a better idea of the situation, let's consider another scenario where the student knew the correct answers to 50 questions.
Here it might seem that if the student knew more,
then the risk of attempting rest of the questions should be lower.
For this is the case, our limiting value is 2 correct guesses as 2⋅4-8⋅1=0,
Surprisingly, here we have only 75% chance to benefit!
So, its actually less than the previous case. So, this definitely doesn't work as I thought it should.
For now, let's stick to our original question,
In the above cases I assumed that the student attempted all the questions which they couldn't solve,
but they don't necessarily have to, so my answer is incomplete.
Now, this question is not out of any textbook so I don't even know that whether this is a valid question,
Of course, even though I don't have an idea that which cases will have a higher probability, I can simply just do all the cases one by one, i.e., we can assume that they attempts all the questions and then find its probability of profit and then similarly we can do this by assuming that they attempted only 14 and then 13... and so on. And Finally we can compare out of all these cases which one has the highest probability of profit.
But I wanted a more generalized approach,
First, because this way we can extend this question to lots of other cases like, what happens when the student knew only 40 out of 60 questions?
We can still do the above process here, but there must be some way to form a function which could altogether give us the probability for all such possible cases.
Second reason is because what I actually want to know is how to maximize your marks in MCQs?
And to answer this question we will have to consider the marks scored by the student as well.
As in the original (made up) question, I only talked about "benefit/profit". Which means that even if the student scored 180 marks or 181 marks, this is considered as profit.
But that does not "maximize" the student's marks.
But again to answer such questions, one doesn't have a definite answer. All we can have is probabilities. This becomes a much harder problem.
So, in the end, I believe that if we could answer the simpler problem (the one in the homework statement), and we could generalize this situation, then maybe we could have a better idea on how to maximize our marks by comparing the situations, this time by taking both the marks scored in a case and the probability to score that marks in that case, into account simultaneously.
This way we could finally say that, yes, even though the probability to "X" marks is low, but the profit here is so high that it should be the best situation!
P.S., I know that the case when the student scores 180 marks is not actually a profit, but I considered this as benefit/profit because if the student doesn't lose marks, they can take this risk and attempt even the questions they couldn't solve. Its a win-win situation for them.
Edit: The question should also include that at least one guess is made by the student.
Attachments
Last edited: