Maximizing the fraction of two integrals using matlab

[Verdict]

EDIT:
I left out something of major importance, I want to maximize with respect to a!

Good day,

I've run into an issue in solving a certain problem with matlab, and I was hoping if anyone could help me out. I am relatively new to matlab, so I don't even know if this is possible, but I figured that in principle it should be.

What I want to do is maximize

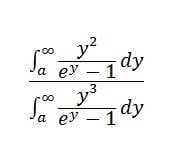
for positive values of a.
With the calculus I know, I can't evaluate these integrals, so I have no applicable formula's so I am pretty stuck at this point. I tried using mathematica, and although it can evaluate the integrals, it cannot maximize the fraction. So instead I figured I should use MATLAB (which I also have to my disposal) to do so instead, but I simply don't know how. I don't get much further than defining the integrals, as
fun1 = @(x) x.^2./(exp(x)-1);
fun2 = @(x) x.^3./(exp(x)-1);

Could anyone help me out?

Kind regards

 

[UltrafastPED]

Given the Mathematica can solve the integrals - then just use a as a parameter and plot the ratio for a running from 0 to 100 by steps of 1 - and look at the plot.

Mathematica will be a better tool for this type of work than Matlab.

 

[kreil]

That's not true at all, MATLAB can handle problems like this just fine.

1. Define the functions. You got this part already.

fun1 = @(x) x.^2./(exp(x)-1);
fun2 = @(x) x.^3./(exp(x)-1);

2. Define the function with a parameter.

q = @(a) integral(fun1,a,Inf)./integral(fun2,a,Inf);

3. Plot the results and read the maximum off the plot.

for j=0:100
    Q(j+1) = q(j);
end
plot(0:100,Q)

The answer is 0, which is rather intuitive when you think about it.