- #1
AppleiPad556
- 8
- 1
- Homework Statement
- (see below)
- Relevant Equations
- ##E_{rotational}=\frac{1}{2}I\omega^2##
##\omega=\frac{\Delta\theta}{{\Delta}t}##
##I=\frac{1}{3}ma^2## (for rectangular plate with axis of rotation along a side)
##E_{spring}=\frac{1}{2}kx^2##
Hello!
I had a random question while playing around with a garbage can that I hoped y'all could help me walk through:
Let's say that I have a hinge on a table, rotating with gravity acting perpendicular to it. Energy is provided into the hinge, let's say by a spring, like so:
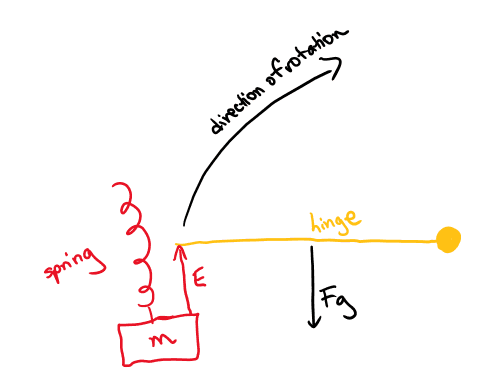
I want to know the maximum angle the hinge will make with the table given a certain amount of energy (ultimately how much energy will cause the hinge to "tip" over 90° and fall over the other direction).
For the energy from the spring, I would set up the spring so that its rest position is in line with the hinge resting position, which means I can start with the maximum kinetic energy:
$$E_{spring}=\frac{1}{2}kx^2$$
Where ##k## is the spring constant and ##x## is the displacement.
However, it's almost certain that the spring will continue to move after impact from the spring, meaning I would have to subtract the energy it has still from this total kinetic energy. Something like:
$$E=\frac{1}{2}kx^2-\frac{1}{2}mv^2$$
We'll let this be ##E##.
Assuming that the hinge has no friction and that all energy is conserved, I begin with the Energy formula for rotational motion:
$$E_{rotational}=\frac{1}{2}I\omega^2$$
Where
$$E_{rotational}=\frac{1}{2}(\frac{1}{3}ma^2)(\frac{\Delta\theta}{{\Delta}t})^2$$
Now ##\Delta\theta## and ##{\Delta}t## both have initial values of ##0##, so I can simply look at their final values.
Solving for ##\theta## I get:
$$\theta=\sqrt{\frac{6Et^2}{ma^2}}$$
My question is whether this logic makes sense and whether it seems reasonable to solve for the angle made by the hinge? Am I missing anything that could also play a role in this? How does gravity come into play?
Thanks!
I had a random question while playing around with a garbage can that I hoped y'all could help me walk through:
Let's say that I have a hinge on a table, rotating with gravity acting perpendicular to it. Energy is provided into the hinge, let's say by a spring, like so:
I want to know the maximum angle the hinge will make with the table given a certain amount of energy (ultimately how much energy will cause the hinge to "tip" over 90° and fall over the other direction).
For the energy from the spring, I would set up the spring so that its rest position is in line with the hinge resting position, which means I can start with the maximum kinetic energy:
$$E_{spring}=\frac{1}{2}kx^2$$
Where ##k## is the spring constant and ##x## is the displacement.
However, it's almost certain that the spring will continue to move after impact from the spring, meaning I would have to subtract the energy it has still from this total kinetic energy. Something like:
$$E=\frac{1}{2}kx^2-\frac{1}{2}mv^2$$
We'll let this be ##E##.
Assuming that the hinge has no friction and that all energy is conserved, I begin with the Energy formula for rotational motion:
$$E_{rotational}=\frac{1}{2}I\omega^2$$
Where
- ##I## is the moment of inertia (in this case, for a rectangular plate with rotation along a side, ##\frac{1}{3}ma^2##, where ##m## is mass and ##a## is length)
- ##\omega## is the angular velocity.
$$E_{rotational}=\frac{1}{2}(\frac{1}{3}ma^2)(\frac{\Delta\theta}{{\Delta}t})^2$$
Now ##\Delta\theta## and ##{\Delta}t## both have initial values of ##0##, so I can simply look at their final values.
Solving for ##\theta## I get:
$$\theta=\sqrt{\frac{6Et^2}{ma^2}}$$
My question is whether this logic makes sense and whether it seems reasonable to solve for the angle made by the hinge? Am I missing anything that could also play a role in this? How does gravity come into play?
Thanks!