Discussion Overview
The discussion revolves around determining the maximum area of a rectangle that can circumscribe a given quadrilateral defined by its diagonal lengths and area. Participants explore various mathematical approaches, including geometry and calculus, to address the problem.
Discussion Character
- Exploratory
- Mathematical reasoning
- Debate/contested
Main Points Raised
- Some participants note that the area of a quadrilateral can be expressed as $$A = \tfrac{1}{2}pq\sin \phi$$, where $$p$$ and $$q$$ are the diagonal lengths and $$\phi$$ is the angle between them.
- Several participants suggest that the maximum area of the circumscribed rectangle could be derived from the properties of the quadrilateral and its diagonals.
- One participant proposes a specific case of a square quadrilateral, concluding that the maximum area of the circumscribed rectangle is $$2A$$, but notes that this does not match any of the provided answer choices.
- Another participant questions the necessity of the angle $$\phi$$ and suggests that it can be derived from the given area and diagonal lengths.
- Some participants express confusion regarding the correct answer from the provided multiple-choice options and seek clarification on how to derive it step by step.
- There are discussions about using derivatives to find maximum areas and the implications of different angles on the area calculations.
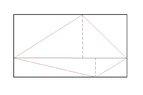
- One participant shares a geometric representation to aid in understanding the problem, indicating a collaborative effort to visualize the solution.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the correct answer to the problem, with multiple competing views on how to approach the solution and differing interpretations of the implications of the given information.
Contextual Notes
The discussion highlights the dependence on the angle $$\phi$$, which is not explicitly provided, leading to uncertainty in deriving the maximum area. There are also unresolved mathematical steps regarding the application of derivatives and the relationships between the variables involved.
Who May Find This Useful
This discussion may be useful for individuals interested in mathematical problem-solving, particularly in the context of geometry and optimization within quadrilaterals.