Maxwell equations in terms of potentials

[olgerm]

These are Maxwell´s equations in potential formulation:

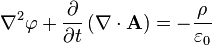
∇²φ = DIV(grad(φ)) . Am I right?
∇²A = ROT(ROT(A))=ROT(B)=grad(DIV(A))-Laplace(A) . Am I right?
In coulomb gauge in every point and at any time DIV(A)=[PLAIN]https://upload.wikimedia.org/math/4/4/1/44131cc26bd9db464d0edb7459ccca84.png. Am I right?
Where could I find Maxwell´s equations in terms of potentials without vector operator?

How must ROT (same as curl) be generalized to make the equations describe EM-field in D-dimensional space equally with these equation
$\begin{cases} & \sum_{i=1}^D(\frac{\partial E_i}{\partial x_i})=\rho \frac{1}{{\epsilon_0}} \\ & \frac{\partial E_a}{\partial t}=\sum_{i=1}^D(\frac{\partial B_{[i;a]}}{\partial x_i})-J_a \\ & \frac{\partial B_{[a;b]}}{\partial t}=\frac{\partial E_b}{\partial x_a}-\frac{\partial E_a}{\partial x_b}\\ & \frac{\partial B_{[a;b]}}{\partial x_c}+\frac{\partial B_{[b;c]}}{\partial x_a}+\frac{\partial B_{[c;a]}}{\partial x_b}=0 \end{cases}$
,which are in terms of E and B?

φ is electripotentialfield.
E is electricvectorfield.
A is magneticpotentialvectorfield.
B is magneticvectorfield.
ρ is electriccharge density.

 

[Khashishi]

∇2φ = DIV(grad(φ)) . Am I right?

Yes

∇2A = ROT(ROT(A))=ROT(B)=grad(DIV(A))-Laplace(A) . Am I right?

No. Look here: https://en.wikipedia.org/wiki/Vector_Laplacian

In coulomb gauge in every point and at any time DIV(A)=

. Am I right?

Yes

Where could I find Maxwell´s equations in terms of potentials without vector operator?

You can do this yourself. Just take what you have above and replace with partial derivatives. Also, this might be useful
https://en.wikipedia.org/wiki/Covariant_formulation_of_classical_electromagnetism

Your last question is a little weird. Are interested in a 2D subset (x,y) of 3D space (x,y,z) where z is a symmetry?

 

[olgerm]

No. Look here: https://en.wikipedia.org/wiki/Vector_Laplacian

It seems to confirm, that ROT(ROT(A))=grad(DIV(A))-Laplace(A) .
also this http://m.wolframalpha.com/input/?i=curl+(curl+A)&x=0&y=0 seems to confirm, that ROT(ROT(A))=grad(DIV(A))-Laplace(A) . Or does ∇² A in the second equation note Laplace(A) not ROT(ROT(A))?

Your last question is a little weird. Are interested in a 2D subset (x,y) of 3D space (x,y,z) where z is a symmetry?

I am interested about theoretical physical system with D-dimensional space. Understanding physical meaning of such system is not necessary to answer the question.

 

[Khashishi]

$\nabla^2 A$ means the same thing as Laplace(A).

How many dimensions do you want to work in?

 

[olgerm]

How many dimensions do you want to work in?

D dimensions. Generalization must include variable D.

 

[olgerm]

Now as I understand there are different Laplacians for vectorfield and scalarfield it makes more sense.

So are these equations in lorenz gauge
$\begin{cases} \frac{\partial^2 A_{D_1}}{\partial t^2}=J_{D_1}\cdot k_E \cdot \pi \cdot c^2 \cdot 4+\sum_{i=1}^D(\frac{\partial^2 A}{\partial x_i \cdot \partial x_{D_1}}) \cdot c^2-ROT(ROT(A)) \cdot c^2\\ \frac{\partial^2 \phi}{\partial t^2}=\rho \cdot k_E \cdot \pi \cdot 4+\sum_{i=1}^D(\frac{\partial^2 \phi}{\partial x_i^2})\\ \frac{\partial \phi}{\partial t}=\sum_{i=1}^D(\frac{\partial A_i}{\partial x_i}) \cdot c^2\\ F_E=q\cdot(\sum_{i=1}^D(v_i \cdot \frac{\partial A_i}{\partial x_{D_1}})-\frac{\partial A_{D_1}}{\partial t}-\frac{\partial \phi}{\partial x_{D_1}}) \end{cases}$
?

But what must ROT(ROT(A)) equal to in D-dimensional space so that the Maxwell equations were equal with these
$\begin{cases} & \sum_{i=1}^D(\frac{\partial E_i}{\partial x_i})=\rho \frac{1}{{\epsilon_0}} \\ & \frac{\partial E_a}{\partial t}=\sum_{i=1}^D(\frac{\partial B_{[i;a]}}{\partial x_i})-J_a \\ & \frac{\partial B_{[a;b]}}{\partial t}=\frac{\partial E_b}{\partial x_a}-\frac{\partial E_a}{\partial x_b}\\ & \frac{\partial B_{[a;b]}}{\partial x_c}+\frac{\partial B_{[b;c]}}{\partial x_a}+\frac{\partial B_{[c;a]}}{\partial x_b}=0 \end{cases}$
equation?
I also want the equation system to be formed as short and easy as possible. What gauge you recommend me to choose? Any ideas how to simplify the equations?

 

[olgerm]

I have hypothesis, that Laplace(A) must be generalized to be equal to $2\cdot\frac{\partial^2 A_{D_1}}{\partial x_{D_1}^2}-\sum_{i=1}^D(\frac{\partial^2 A_{D_1}}{\partial x_i^2})$ .
Can anybody check if it is correct?

 

[Khashishi]

You know what the electromagnetic tensor is? You should use a tensor formulation if you want to generalize to different dimensions. I asked what dimension you wanted to work in because it affects the answer. Cross product only really works in 3 or 7 dimensions. You might want to use the Levi-Civita symbol.

 

[olgerm]

You know what the electromagnetic tensor is? You should use a tensor formulation if you want to generalize to different dimensions.

I got the equations in E and B formulation from Maxwell equations in electromagnetic tensor formulation.

The equations should not contain vector products on operators, but partial derivatives and sums. D must be a variabe, that can be equal to any natural number.

 

[olgerm]

I have got my answer. Correct equation system is:
$\begin{cases} \frac{\partial^2 A_{D_1}}{\partial t^2}=J_{D_1}\cdot k_E \cdot \pi \cdot 4+\sum_{i=1}^D(\frac{\partial^2 A_{D_1}}{\partial x_i^2}) \cdot c^2\\ \frac{\partial^2 \phi}{\partial t^2}=\rho \cdot k_E \cdot c^2 \cdot \pi \cdot 4+\sum_{i=1}^D(\frac{\partial^2 \phi}{\partial x_i^2})\\ \frac{\partial \phi}{\partial t}=\sum_{i=1}^D(\frac{\partial A_i}{\partial x_i}) \cdot c^2\\ F_E=q\cdot(\sum_{i=1}^D(v_i \cdot \frac{\partial A_i}{\partial x_{D_1}})-\frac{\partial A_{D_1}}{\partial t}-\frac{\partial \phi}{\partial x_{D_1}}) \end{cases}$