Maya's question at Yahoo Answers regarding a Riemann sum and definite integral

[MarkFL]

Here is the question:

I need some help with calculus 1 please?

Here's my problem:
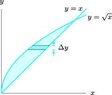
Write a Riemann sum and then a definite integral representing the area of the region, using the strip shown in the figure below. Evaluate the integral exactly.

View attachment 1138

What is the approximate area of the strip with respect to y? (Use Delta y for Δy as necessary.)

In your definite integral what is the upper endpoint given that the lower endpoint is 0?

and finally, what is the result when you evaluate the definite integral?

10 points to best answer! Thanks!

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Maya,

I will choose to use the lower end of each strip to determine its width.

For an arbitrary strip, its area can be found as follows:

$$A_k=bh$$

where:

$$y_k=k\frac{y_n-y_0}{n}=k\frac{1-0}{n}=\frac{k}{n}$$

$$b=y_k-y_k^2=\frac{nk-k^2}{n^2}$$

$$h=\Delta y=y_{k+1}-y_{k}=\frac{1}{n}$$

and so we have:

$$A_k=\left(y_k-y_k^2 \right)\Delta y=\frac{nk-k^2}{n^3}$$

Now, summing the strips, we find:

$$A_n=\sum_{k=0}^{n-1}\left(\frac{nk-k^2}{n^3} \right)=\frac{1}{n^3}\sum_{k=0}^{n-1}\left(nk-k^2 \right)$$

Using the following identities:

$$\sum_{k=0}^{n-1}(k)=\frac{n(n-1)}{2}$$

$$\sum_{k=0}^{n-1}(k^2)=\frac{n(n-1)(2n-1)}{6}$$

we obtain:

$$A_n=\frac{1}{n^3}\left(\frac{n^2(n-1)}{2}-\frac{n(n-1)(2n-1)}{6} \right)$$

$$A_n=\frac{1}{n^3}\left(\frac{n\left(n^2-1 \right)}{6} \right)=\frac{n^2-1}{6n^2}$$

Thus, when we write the definite integral and evaluate it, we should find it is equal to:

$$A=\lim_{n\to\infty}A_n=\frac{1}{6}$$

Now, to represent the area as a definite integral, we may use:

$$A=\int_0^1 y-y^2\,dy=\left[\frac{y^2}{2}-\frac{y^3}{3} \right]_0^1=\frac{1}{6}\left[3y^2-2y^3 \right]_0^1=\frac{1}{6}((3-2)-(0-0))=\frac{1}{6}$$