Measurable Functions .... Lindstrom, Proposition 7.3.7 .... ....

[Math Amateur]

I am reading Tom L. Lindstrom's book: Spaces: An Introduction to Real Analysis ... and I am focused on Chapter 7: Measure and Integration ...

I need help with the proof of Proposition 7.3.7 ...

Proposition 7.3.7 and its proof read as follows:

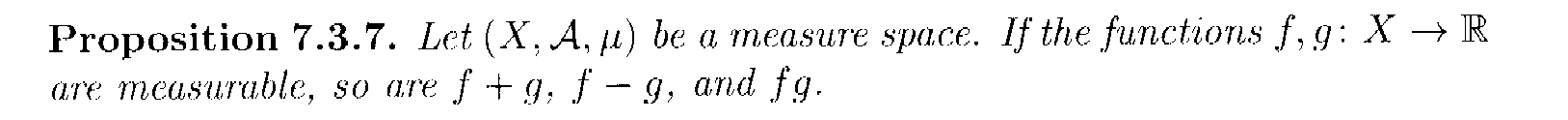
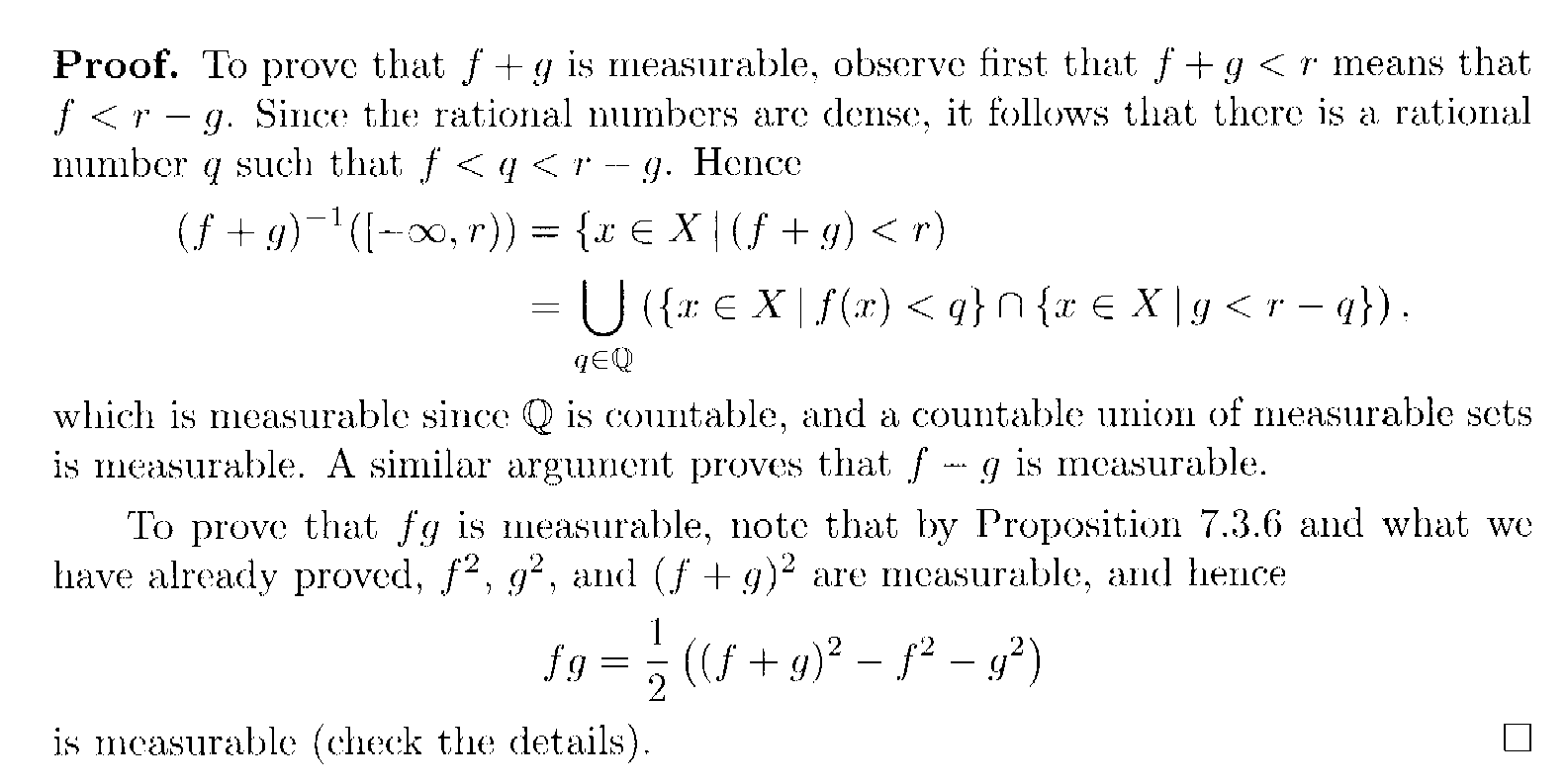
In the above proof by Lindstrom we read the following:

" ... ... \(\displaystyle (f + g)^{ -1} ( [ - \infty , r ) ) = \{ x \in X | (f + g) \lt r \}\)

\(\displaystyle = \bigcup_{ q \in \mathbb{Q} } ( \{ x \in X | f(x) \lt q \} \cap \{ x \in X | g \lt r - q \} )\) ... ... " Can someone please demonstrate, formally and rigorously, how/why ...

\(\displaystyle \{ x \in X | (f + g) \lt r \} = \bigcup_{ q \in \mathbb{Q} } ( \{ x \in X | f(x) \lt q \} \cap \{ x \in X | g \lt r - q \} )\) ... ...Help will be much appreciated ...

Peter=============================================================================================================Readers of the above post may be assisted by access to Lindstrom's introduction to measurable functions (especially Lindstrom's definition of a measurable function, Definition 7.3.1) ... so I am providing access to the relevant text ... as follows:

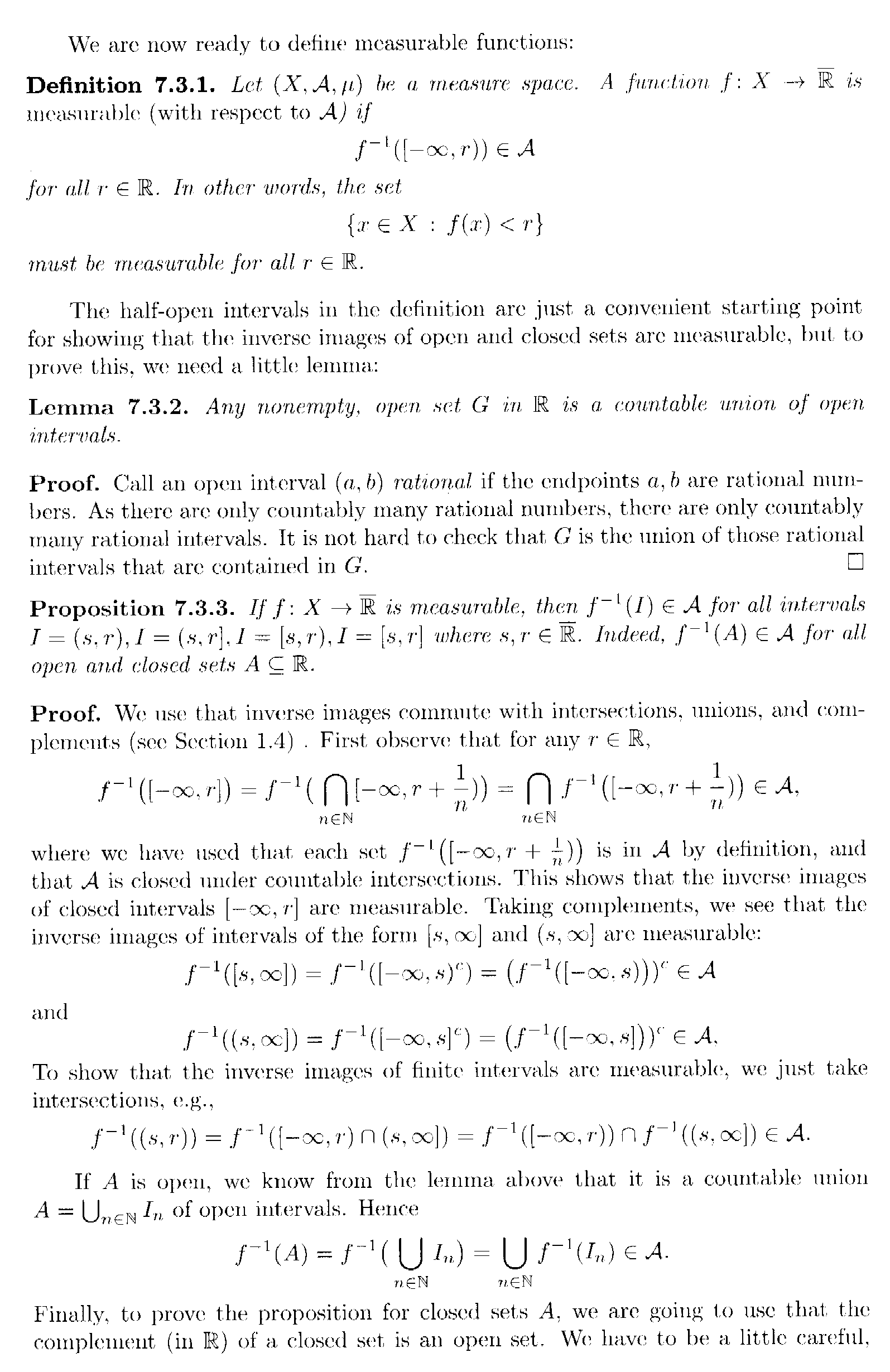
Hope that helps ...

Peter

 

[Evgeny.Makarov]

Have you tried proving mutual inclusion?

 

[Math Amateur]

Hi Evgeny ...

... can you please expand on what you mean ... I’m a bit lost ...

Peter

 

[Evgeny.Makarov]

Don't you know that $A=B\iff A\subseteq B\land B\subseteq A$ and $X\subseteq Y\iff\forall x.\,x\in X\implies x\in Y$?

 

[Math Amateur]

Oh sorry ... yes, indeed, understand that...

... will try following your suggestion...

Thanks for the help ...

Peter

 

[Math Amateur]

I have been reflecting on proving that \(\displaystyle f+ g\) is measurable when \(\displaystyle f\) and \(\displaystyle g\) are measurable ... and I need to clarify an issue before trying the mutual inclusion argument ...

I need to understand exactly what is wrong with the following argument ... something surely is wrong because the proof doesn't involve ranging over \(\displaystyle \mathbb{Q}\) ...

... ... ... the argument follows ... ...First note that \(\displaystyle f + g \lt r \)

\(\displaystyle \Longrightarrow\) there exists \(\displaystyle q \in \mathbb{Q}\) such that \(\displaystyle f \lt q \lt r - g\)

\(\displaystyle \Longrightarrow f \lt q\) and \(\displaystyle g \lt r - q\)

\(\displaystyle \Longrightarrow\) for all \(\displaystyle x \in X\) we have \(\displaystyle f(x) \lt q\) and \(\displaystyle g(x) \lt r - q\)

Thus \(\displaystyle \{ x \in X \ | \ (f + g) \lt r \} = \{ x \in X \ | \ f(x) \lt q \} \cap \{ x \in X \ | \ g(x) \lt r - q \}\)Can someone please clarify what is wrong with the above argument ...Help will be much appreciated ...

Peter

 

[Opalg]

I have been reflecting on proving that \(\displaystyle f+ g\) is measurable when \(\displaystyle f\) and \(\displaystyle g\) are measurable ... and I need to clarify an issue before trying the mutual inclusion argument ...

I need to understand exactly what is wrong with the following argument ... something surely is wrong because the proof doesn't involve ranging over \(\displaystyle \mathbb{Q}\) ...

... ... ... the argument follows ... ...First note that \(\displaystyle f + g \lt r \)

\(\displaystyle \Longrightarrow\) there exists \(\displaystyle q \in \mathbb{Q}\) such that \(\displaystyle f \lt q \lt r - g\)

\(\displaystyle \Longrightarrow f \lt q\) and \(\displaystyle g \lt r - q\)

\(\displaystyle \Longrightarrow\) for all \(\displaystyle x \in X\) we have \(\displaystyle f(x) \lt q\) and \(\displaystyle g(x) \lt r - q\)

Thus \(\displaystyle \{ x \in X \ | \ (f + g) \lt r \} = \{ x \in X \ | \ f(x) \lt q \} \cap \{ x \in X \ | \ g(x) \lt r - q \}\)Can someone please clarify what is wrong with the above argument ...Help will be much appreciated ...

Peter

Your argument correctly shows that if $(f+g)(x)<r$ then there exists $q \in \mathbb{Q}$ such that \(\displaystyle f(x) \lt q\) and \(\displaystyle g(x) \lt r - q\). But the choice of $q$ depends on $x$. If you want to eliminate that dependency you then have to take the union of all $q\in\Bbb{Q}$, to get \(\displaystyle \{ x \in X | (f + g) \lt r \} \subseteq \bigcup_{ q \in \mathbb{Q} } ( \{ x \in X | f(x) \lt q \} \cap \{ x \in X | g \lt r - q \} )\).

Lindstrom conceals this difficulty by using the horrible notation $f+g<r$ rather than $(f+g)(x)<r$, which disguises the fact that as $x$ varies so does $q$.

 

[Math Amateur]

Thanks for the help Opalg ...

I can see \(\displaystyle q\) may depend on \(\displaystyle x\) ... but cannot see why a union over all \(\displaystyle \mathbb{Q}\) resolves this issue ...

... why are we justified in taking a union over all \(\displaystyle \mathbb{Q}\) ...

Can you explain further ...

Peter

 

[Opalg]

Thanks for the help Opalg ...

I can see \(\displaystyle q\) may depend on \(\displaystyle x\) ... but cannot see why a union over all \(\displaystyle \mathbb{Q}\) resolves this issue ...

... why are we justified in taking a union over all \(\displaystyle \mathbb{Q}\) ...

Can you explain further ...

Peter

I'll try to make it clearer by putting a subscript $0$ for a particular point $x_0$ and a particular rational number $q_0$.

You have shown that, given $x_0\in X$ satisfying $(f+g)(x_0)<r$, there exists $q_0\in\Bbb{Q}$ such that $$x_0 \in \{ x \in X | f(x) \lt q_0 \} \cap \{ x \in X | g \lt r - q_0 \} \subseteq \bigcup_{ q \in \mathbb{Q} } ( \{ x \in X | f(x) \lt q \} \cap \{ x \in X | g \lt r - q \} ).$$ Since that holds for all $x_0$ satisfying $(f+g)(x_0)<r$, it follows that $$\{x\in X | (f+g)(x)<r\} \subseteq \bigcup_{ q \in \mathbb{Q} } ( \{ x \in X | f(x) \lt q \} \cap \{ x \in X | g \lt r - q \} ).$$

(You still have to prove the reverse inclusion, as Evgeny suggests. But that should not be difficult.)