Like Tony Stark
- 182
- 6
- Homework Statement
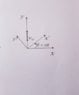
- A particle moves with constant velocity ##v_0## in the ##y## direction with respect to an inertial system ##A(x;y;z)## as depicted in the picture. There is another system ##B(x′;y′;z′)##, which is not inertial and rotates with constant angular velocity ω.
Determine
I) ##r(t)## from the perspective of ##B## and ##A##
II) the velocity measured from ##B##, i.e., the velocity relative to ##B##
III) the acceleration measured from ##B##, i.e., the acceleration relative to ##B##
- Relevant Equations
- Relative motion equations for non inertial reference frame
I) For ##A##, the positition is ##\vec r=(0;V_0 . t;0)##.
For ##B##, we have ##\vec r_A=\vec r_B + \vec r_{A/B}##, but ##\vec r_{A/B}## is equal to zero because they have the same origin, so the position measured from ##A## is equal to the position measured from ##B##
II) For ##A##, velocity is equal to ##V_0##.
For ##B## we know that ##\vec V_A = \vec V_B +\vec \omega \times \vec V_{rel}##. ##\vec V_A## is equal to ##(0;V_0;0)##; ##\vec V_B=0##, since the origin doesn't move; ##\vec \omega## is equal to ##(0;0;\theta /t)##, ##\vec r## is the vector calculated previously and then I solve for ##\vec V_{rel}##.
III) For acceleration we just have to replace the values in the formula and solve for ##\vec a_{rel}##
Is this ok?
For ##B##, we have ##\vec r_A=\vec r_B + \vec r_{A/B}##, but ##\vec r_{A/B}## is equal to zero because they have the same origin, so the position measured from ##A## is equal to the position measured from ##B##
II) For ##A##, velocity is equal to ##V_0##.
For ##B## we know that ##\vec V_A = \vec V_B +\vec \omega \times \vec V_{rel}##. ##\vec V_A## is equal to ##(0;V_0;0)##; ##\vec V_B=0##, since the origin doesn't move; ##\vec \omega## is equal to ##(0;0;\theta /t)##, ##\vec r## is the vector calculated previously and then I solve for ##\vec V_{rel}##.
III) For acceleration we just have to replace the values in the formula and solve for ##\vec a_{rel}##
Is this ok?