Mechanical Advantage vs. Lever vs. Human Error

[BMR]

This is my first post here, so pardon if forum guidelines/criteria require this to be designated elsewhere.

I am designing a clamp mechanism utilizing lever mechanics, and I am getting conflicting info regarding Mechanical Advantage and the Law of 1st Class Levers. Regarding MA, knowing that

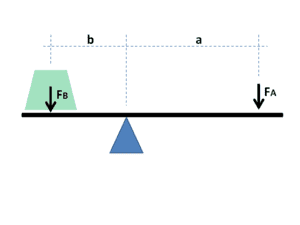
If:
F_B = 40,000 lbs
F_A = 1,000 lbs
Then: b = 40, a = 1, and the MA is 40:1

In regards to Levers (Specifically 1st Class Levers)

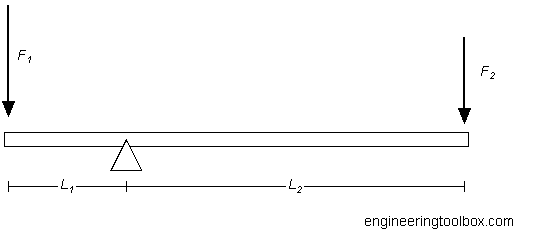
F₂ = F₁ L₁ / L₂

If:
F_B = 40,000 lbs
F_A = 1,000 lbs

Then:
40,000 = 1,000 (32.174 ft/s² [gravity constant]) (L₁ / L₂)
40 = 32.174 (L₁ / L₂)
L₁ / L₂ = approx. 1.243 or 1.243:1.

So for 1,000 lbs to lift 40,000 lbs., either a 40:1 or 1.243:1 lever ratio is required. Am I simply wrong for factoring in a gravitational constant?

 

[kuruman]

Am I simply wrong for factoring in a gravitational constant?

Yes. You get the same mechanical advantage whether the lever is on the Earth, the Moon or in free space.

On Edit: Assuming that F₁ and F₂ are either both pushing forces or both weights, that is.

 

[anorlunda]

So for 1,000 lbs to lift 40,000 lbs., either a 40:1 or 1.243:1 lever ratio is required.

@kuruman gave you the correct answer. But to amplify, if you move the whole apparatus to a planet with one half Earth's gravity, then the same weights would weigh 500 lbs and 20000 lbs, but the ratio 40:1 remains unchanged and the MA remains unchanged. That is why you don't need G.

 

[kuruman]

Another way to say the same thing as @anorlunda: If the number 1000 is a mass, then you multiply by g to get a weight which is a force. Here you have 1000 lbs which is already a force (the mass has already been multiplied by g) so it would be wrong to multiply by g again.