Discussion Overview
The discussion revolves around applying the method of least squares to determine the initial position and velocity of a point moving linearly with constant velocity, described by the equation \(x = a + vt\). Participants explore how to set up the problem using given data and the least squares method, including the formulation of a linear system.
Discussion Character
- Exploratory
- Mathematical reasoning
- Debate/contested
Main Points Raised
- Some participants propose using the method of least squares to minimize the sum of squared deviations to find \(a\) and \(v\).
- One participant questions the definition of "initial position," suggesting it is directly given as \(x(0) = 1\) from the data.
- Another participant clarifies that the approximation of \(a\) is based on linear least squares interpolation, aiming for a more accurate estimate than the given measurement.
- Participants discuss the formulation of the sum of squared deviations and how to minimize it with respect to \(a\) and \(v\).
- One participant presents a detailed calculation of the partial derivatives of the sum of squared deviations and proposes values for \(a\) and \(v\) based on setting these derivatives to zero.
- Another participant expresses confidence in the correctness of the calculations presented.
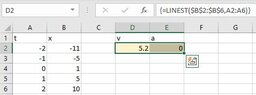
- Some participants mention the use of Excel's LINEST function as an alternative method to obtain results.
Areas of Agreement / Disagreement
There is no clear consensus on the interpretation of "initial position," with differing views on whether it is simply the given data point or requires further calculation. The mathematical approach using least squares is generally accepted, but the discussion remains open regarding the best methods and interpretations.
Contextual Notes
Participants express uncertainty about the assumptions underlying the initial position and the implications of using the least squares method. The discussion includes various approaches and calculations that have not been definitively resolved.
Who May Find This Useful
Readers interested in mathematical modeling, data fitting techniques, or the application of least squares in physics and engineering contexts may find this discussion relevant.