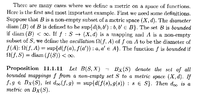Metric Spaces .... the Uniform Metric .... Garling, Proposition 11.1.11 ....

[Math Amateur]

I am reading D. J. H. Garling's book: "A Course in Mathematical Analysis: Volume II: Metric and Topological Spaces, Functions of a Vector Variable" ... ...

I am focused on Chapter 11: Metric Spaces and Normed Spaces ... ...

I need some help with an aspect of the proof of Theorem 11.1.11 ...

Garling's statement and proof of Theorem 11.1.11 reads as follows:
View attachment 8945
View attachment 8946Near the end of Garling's proof above we read the following:

" ... ... Suppose that $$f,g,h \in B_X(S)$$ and that $$s \in S$$. Then

$$d(f(s), h(s)) \le d(f(s), g(s)) + d(g(s), h(s)) \le d_\infty (f, g) + d_\infty (g, h)$$ ... ... ... (1)

Taking the supremum, $$d_\infty (f, h) \le d_\infty (f, g) + d_\infty (g, h)$$ ... ... ... "Now (1) is true for arbitrary s and so it is true for all $$s$$ including the point for which $$d(f(s), h(s))$$ is a maximum ... if a maximum exists ...But in the case where a maximum does not exist ... how do we know that taking the supremum preserves inequality (1) ...Hope someone can help ...

Peter

 

[Opalg]

Near the end of Garling's proof above we read the following:

" ... ... Suppose that $$f,g,h \in B_X(S)$$ and that $$s \in S$$. Then

$$d(f(s), h(s)) \le d(f(s), g(s)) + d(g(s), h(s)) \le d_\infty (f, g) + d_\infty (g, h)$$ ... ... ... (1)

Taking the supremum, $$d_\infty (f, h) \le d_\infty (f, g) + d_\infty (g, h)$$ ... ... ... "Now (1) is true for arbitrary s and so it is true for all $$s$$ including the point for which $$d(f(s), h(s))$$ is a maximum ... if a maximum exists ...But in the case where a maximum does not exist ... how do we know that taking the supremum preserves inequality (1) ...

The inequality (1) shows that $d_\infty (f, g) + d_\infty (g, h)$ is an upper bound for $d(f(s), h(s))$. The supremum (or least upper bound) of $d(f(s), h(s))$ must therefore be at most $d_\infty (f, g) + d_\infty (g, h)$.

 

[Math Amateur]

The inequality (1) shows that $d_\infty (f, g) + d_\infty (g, h)$ is an upper bound for $d(f(s), h(s))$. The supremum (or least upper bound) of $d(f(s), h(s))$ must therefore be at most $d_\infty (f, g) + d_\infty (g, h)$.[Thanks for clarifying the issue Opalg ...

Appreciate your help...

Peter