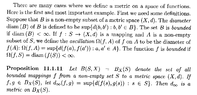Norm bounded Sets .... remarks by Garling in Section 11.2 Normed Spaces ....

[Math Amateur]

I am reading D. J. H. Garling's book: "A Course in Mathematical Analysis: Volume II: Metric and Topological Spaces, Functions of a Vector Variable" ... ...

I am focused on Chapter 11: Metric Spaces and Normed Spaces ... ...

I need some help in order to understand some remarks by Garling on norm bounded sets made in Section 11.2 on page 311 ... ...

The remarks by Garling made in Section 11.2 on page 311 ... ... read as follows:

View attachment 8995
In the above text from Garling we read the following ...

" ... Arguing as in Proposition 11.1.11,

$$\| f \|_\infty = d_\infty ( f, 0 ) = \text{sup} \{ \| f(s) \| \ : \ s \in S \} $$

is a norm on $$B_E(S)$$ ... ... "I am able to prove two of the conditions for a norm, but am unsure how to formally and rigorously demonstrate that

$$\| \lambda f \|_\infty = \mid \lambda \mid \| f \|_\infty$$
Can someone please help ...
My thoughts so far are as follows:

$$\| \lambda f \|_\infty = d_\infty ( \lambda f, 0 ) = \text{sup} \{ d ( ( \lambda f ) (s) , 0 ) \}$$

$$= \text{sup} \{ d ( \lambda f (s) , 0 ) \}$$ ... ...

But where to from here ... and how do we justify the steps we take?
Hope someone can help ...

Peter
==========================================================================================
The above post mentions Proposition 11.1.11 ... so I am providing text of the same plus some relevant preceding remarks ... as follows ...
View attachment 8996
View attachment 8997
Hope that helps ...

Peter

 

[Opalg]

I am able to prove two of the conditions for a norm, but am unsure how to formally and rigorously demonstrate that

$$\| \lambda f \|_\infty = \mid \lambda \mid \| f \|_\infty$$

My thoughts so far are as follows:

$$\| \lambda f \|_\infty = d_\infty ( \lambda f, 0 ) = \text{sup} \{ d ( ( \lambda f ) (s) , 0 ) \}$$

$$= \text{sup} \{ d ( \lambda f (s) , 0 ) \}$$ ... ...

$d( ( \lambda f ) (s) , 0 ) = \|( \lambda f ) (s) - 0 \| = \| \lambda (f (s)) \| = |\lambda|\|f(s)\|$.

Then when you take the sup, $\sup\{ d( ( \lambda f ) (s) , 0 )\} = \sup\{|\lambda|\|f(s)\|\} = |\lambda|\sup\{\|f(s)\|\} = |\lambda|\|f\|_\infty.$

 

[Math Amateur]

$d( ( \lambda f ) (s) , 0 ) = \|( \lambda f ) (s) - 0 \| = \| \lambda (f (s)) \| = |\lambda|\|f(s)\|$.

Then when you take the sup, $\sup\{ d( ( \lambda f ) (s) , 0 )\} = \sup\{|\lambda|\|f(s)\|\} = |\lambda|\sup\{\|f(s)\|\} = |\lambda|\|f\|_\infty.$

Thanks Opalg ... appreciate the help ...

Peter