Midpoint Formula: Deriving & Understanding

  • Context: High School 
  • Thread starter Thread starter Meepers
  • Start date Start date
Click For Summary
SUMMARY

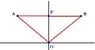
The discussion focuses on deriving the midpoint and centroid of a triangle using specific vertex coordinates. The centroid of a triangle with vertices A(-a, b), B(a, b), and C(0, 0) is calculated by averaging the coordinates, resulting in the formula (0, (2/3)b). This method is effective for triangles but does not apply to polygons with more than three sides. The conversation highlights the importance of understanding geometric properties when calculating centroids.

PREREQUISITES
  • Understanding of basic geometry concepts, particularly triangles
  • Familiarity with coordinate systems and vertex notation
  • Knowledge of averaging techniques in mathematics
  • Ability to differentiate between midpoint and centroid calculations
NEXT STEPS
  • Research the properties of centroids in polygons with more than three sides
  • Learn about the midpoint formula in coordinate geometry
  • Explore applications of centroids in physics and engineering
  • Study advanced geometric concepts such as barycentric coordinates
USEFUL FOR

Students, educators, and professionals in mathematics, geometry, and engineering who seek to deepen their understanding of geometric properties and calculations related to triangles and centroids.

Meepers
Messages
2
Reaction score
0
Figured out, thanks.
 

Attachments

  • derivemidpoint.JPG
    derivemidpoint.JPG
    6.3 KB · Views: 479
Last edited:
Mathematics news on Phys.org
I need more information. Find the midpoint of what? Do you mean find the centroid of the triangle? Assuming that line AB is horizontal and P is the midpoint of AB, then the centroid is on the line OP.

One very nice method of finding the centroid of a triangle (doesn't work for figures of more than three sides) is to "average" the three vertices. That is, if the vertices of this triangle are A(-a, b), B(a, b), C(0,0) as it appears, then the centroid is a ((-a+a+ 0)/3, ((b+b+0)/3)= (0, (2/3)b).
 
Its okay, I've figured it out, thank you though.
 

Similar threads

Undergrad Introducing integral in textbooks
  • · Replies 8 ·
Replies
8
Views
963
MHB Dividing Line Segments into Four Equal Parts using Midpoint Formula
  • · Replies 5 ·
Replies
5
Views
2K
MHB How to Use the Midpoint Formula to Find the Other Endpoint of a Line Segment?
  • · Replies 9 ·
Replies
9
Views
2K
High School Are there English names for these formulas? (binomial formulas)
  • · Replies 42 ·
2
Replies
42
Views
5K
MHB How do I use the midpoint formula to find the coordinates of point C?
  • · Replies 2 ·
Replies
2
Views
6K
High School Understanding the Relationship Between a Function and Its Inverse
  • · Replies 11 ·
Replies
11
Views
2K
High School A Simpler Way to Find the Shaded Area?
  • · Replies 1 ·
Replies
1
Views
2K
High School Can Higher Degree Nested Radicals Be Simplified?
  • · Replies 41 ·
2
Replies
41
Views
6K
MHB Proof of Parallelogram ABCD: Midpoint X & Y Show Area $\frac{1}{4}$
  • · Replies 5 ·
Replies
5
Views
2K
High School A triangle problem: Prove that |AC|+|AB|=|PR|+|PQ| given some constraints
  • · Replies 13 ·
Replies
13
Views
3K