Missle Defense System (Projectile Motion)

In summary, the design of a missile defense system involves using a Patriot Rocket to shoot down incoming missiles that pass over a perimeter defense post. The Patriot Rocket must be set at an angle of θ = 62.0 degrees from vertical and have a magnitude of acceleration given by a = A(e^-bt), where A is a variable that can be set when the rocket is fired and b = 0.15 s^-1. To hit an incoming missile traveling at a constant speed of 799.0 m/s and passing over the defense base at a height of 4.50 km, the value of A must be determined. This will require solving for the time ∆t in between launch and impact, as well as the
  • #1
dlee9
3
0
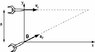
You are designing a missile defense system that will shoot down incoming missiles that pass over a perimeter defense post. The set-up is shown below. An incoming missile passes directly above the defense base. Radar at the base can measure the height, h, and speed, v1, of the incoming missile. Your Patriot Rocket is set to fire at an angle of θ = 62.0 degrees from vertical. You design the Patriot Rocket so the magnitude of its acceleration is given by:

a = A(e^−bt)

where A can be set on your Patriot Rocket as it is fired, and b = 0.15 s-1. The direction of your Patriot Rocket's vector acceleration stays at the same angle, θ, for the entire trip. If an incoming missile passes over the defense base at a height of 4.50 km and at a constant speed of 799.0 m/s (this means that v1 is constant), solve for the value of A your Patriot Rocket must have in order to hit the incoming missile. You will also need to enter results from intermediate steps of your calculation, including the time ∆t in between launch and impact, and the horizontal distance ∆x from the launch station to the impact position.

Homework Equations

The Attempt at a Solution


I'm stuck at even where to begin. I was thinking of taking the integral of the acceleration but I still am left with 2 unknowns in 1 equation.
 

Attachments

  • MissileDefenseSystem.jpg
    MissileDefenseSystem.jpg
    7 KB · Views: 451
Physics news on Phys.org
  • #2
dlee9 said:
to begin. I was thinking of taking the integral of the acceleration but I still am left with 2 unknowns in 1 equation
There are two dimensions, so two equations. Please post your working as far as you get.
 

1. What is a Missle Defense System?

A Missle Defense System is a defense mechanism designed to intercept and destroy incoming missiles or other projectiles before they reach their intended target. It is a complex system that involves various technologies and strategies to detect, track, and eliminate threats.

2. How does a Missle Defense System work?

A Missle Defense System uses a combination of sensors, radars, and interceptors to detect and track incoming missiles. Once a threat is identified, the system calculates the trajectory and uses interceptors to destroy the missile before it reaches its target. The interceptors can be launched from land, sea, or air depending on the location and type of threat.

3. What are the advantages of having a Missle Defense System?

A Missle Defense System provides a layer of protection against potential missile attacks, which can prevent significant damage and loss of life. It also serves as a deterrent to potential aggressors, as they know their missiles can be intercepted and neutralized. Additionally, a Missle Defense System can enhance a country's defense capabilities and increase national security.

4. Are there any limitations to Missle Defense Systems?

While Missle Defense Systems are highly advanced, they are not foolproof and have some limitations. They may not be able to intercept all types of missiles, especially those with advanced technology. The system's effectiveness also depends on factors such as the speed and trajectory of the missile, weather conditions, and the number of interceptors available. Additionally, Missle Defense Systems can be costly to develop and maintain.

5. Are there any ethical concerns surrounding Missle Defense Systems?

There have been debates about the ethical implications of Missle Defense Systems. Some argue that these systems can escalate tensions between countries and lead to an arms race. Others raise concerns about the potential for false alarms and the unintentional destruction of innocent targets. However, proponents argue that Missle Defense Systems are necessary for national defense and can potentially save lives in the event of an attack.

Similar threads

Missile Defense System - Collide Missiles
    • Introductory Physics Homework Help
Replies
4
Views
5K
Missle Defense System (Projectile Motion)
    • Introductory Physics Homework Help
Replies
2
Views
8K
Hitting a rocket with a projectile
    • Introductory Physics Homework Help
2
Replies
53
Views
3K
Projectile motion submarine missle problem
    • Introductory Physics Homework Help
Replies
13
Views
2K
Exploring the Acceleration of a Projectile Motion Lab
    • Introductory Physics Homework Help
Replies
8
Views
2K
Relationship between Launch height and range of a projectile
    • Introductory Physics Homework Help
Replies
15
Views
21K
Projectile Motion with Pulley System
    • Introductory Physics Homework Help
Replies
3
Views
963
Projectile Motion Max Height and Range
    • Introductory Physics Homework Help
Replies
1
Views
2K
Compute the angle θ that will maximize the height of h of the impact point
    • Introductory Physics Homework Help
Replies
8
Views
4K
Projectile motion above ground given only angle and height
    • Introductory Physics Homework Help
Replies
3
Views
1K

Hot Threads

Recent Insights

Back
Top