MIT OCW 8.02 Electromagnetism: how were these two limits calculated?

[zenterix]

Homework Statement

I'm having a bit of trouble with calculating two specific limits.

Here is some context about where the limits came from, though my question is strictly about how to calculate the limits.

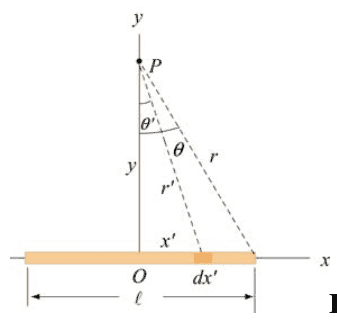
I was asked to calculate the electric field at a point $P$, located a distance $y$ from the center of a rod along its perpendicular bisector (see image below).

Relevant Equations

The answer is the following expression for the electric field at point $P$:

$$\vec{E}_p=\frac{k_eQ}{y\sqrt{y^2+\frac{l^2}{4}}}\hat{j}$$

I would like to calculate the limit of this expression in two edge cases:

1) $y>>l$
2) $l>>y$

The answers are $\frac{k_eQ}{y^2}\hat{j}$ and $\frac{2k_e \lambda}{y}\hat{j}$, respectively, where $\lambda$ is simply the linear density of the rod, ie $\frac{Q}{l}$ (again, this is just for context).

I know what the answers are, because this is all part of the notes from MIT OCW's 8.02 Electromagnetism course. In case you want to see the actual problem, it is example 2.3 that starts on page 18; the limits I am asking about are on page 20.

How do I go about calculating the limits? Ie, what is the name of the specific technique from Calculus used to solve them? I think it might be a Taylor expansion of part of the denominator of the expression for $\vec{E}_p$.

 

[PeroK]

The technique here would be to express your equation in terms of the dimensionless quantities $l/y$ or $y/l$. In each case, $l >> y$ or $y >> l$ imply that $y/l$ or $l/y$ are approximately zero.

 

[zenterix]

$$E_p = \frac{k_eQ}{y\sqrt{y^2+\frac{l^2}{4}}}$$
$$=\frac{k_eQ}{y\sqrt{y^2(1+\frac{l^2}{4y^2})}}$$
$$=\frac{k_eQ}{y^2\sqrt{1+\frac{l^2}{4y^2}}}$$

Here we have a ratio of two functions. Say we'd like to know what happens if $y>>l$.

From inspection we can see that there is a $y^2$ term and a term that approaches $1$ in the square root.

Actually, now it seems to me that we're not really after the limit $\lim_{y \to \infty}E_p$ because this limit is simply $0$. What we're doing seems to be what I initially guessed which is somehow using a linear approximation of the $\sqrt{1+\frac{l^2}{4y^2}}$ term to conclude that when $y>>l$ we have

$$s=\frac{l}{2y}$$
$$1+(\frac{l}{2y})^2=1+s^2 = f(s)$$
$$y>>l \implies s \approx 0$$
$$\implies f(s) \approx f(0) +f'(0)s,\text{ near s=0}$$
$$\implies f(s) \approx 1$$
$$E_p \approx \frac{k_e Q}{y^2}$$

The notes explicitly say "in the limit where $y>>l$", but now that seems inaccurate. Am I right or wrong about this?

 

[PeroK]

The notes explicitly say "in the limit where $y>>l$", but now that seems inaccurate. Am I right or wrong about this?

Perhaps that's loose language. You could say "in the limit as $\frac l y \rightarrow 0$", which is what $y >> l$ means. In any case, I don't see it as something to get confused about.

$$=\frac{k_eQ}{y^2\sqrt{1+\frac{l^2}{4y^2}}}$$

You should be able to go straight from there to $$=\frac{k_eQ}{y^2} \ \ (y >> l)$$

 

[zenterix]

Perhaps that's loose language. You could say "in the limit as $\frac l y \rightarrow 0$", which is what $y >> l$ means. In any case, I don't see it as something to get confused about. You should be able to go straight from there to $$=\frac{k_eQ}{y^2} \ \ (y >> l)$$

Indeed it is the limit as $\frac{l}{y}$. Out of curiosity are you able to show how to do the Taylor expansion of the denominator $(1+\frac{l}{y})^{1/2}$? This is the first time I am trying to use Taylor Expansion outside of calculus, having a hard time doing it for this, and it is indeed a technique I've seen used with such fractions to investigate such scenarios as $y>>l$.

 

[PeroK]

Indeed it is the limit as $\frac{l}{y}$. Out of curiosity are you able to show how to do the Taylor expansion of the denominator $(1+\frac{l}{y})^{1/2}$? This is the first time I am trying to use Taylor Expansion outside of calculus, having a hard time doing it for this, and it is indeed a technique I've seen used with such fractions to investigate such scenarios as $y>>l$.

That's a particular case called the binomial theorem (for fractional powers):

https://brilliant.org/wiki/fractional-binomial-theorem/

In this case, we have $x = \frac l y$.

That said, you only need an expansion when you want to keep at least first order terms in $\frac l y$. We have:
$$ (1+\frac{l}{y})^{1/2} = 1 + \frac 1 2 (\frac l y) + \frac{\frac 1 2 (-\frac 1 2)}{2!}(\frac l y)^2 \dots \approx 1 + \frac 1 2 (\frac l y) - \frac 1 8 (\frac l y)^2$$
That's called the expansion to second order - i.e. up to an including the term in $(\frac l y)^2$.

The first order expansion would be
$$ (1+\frac{l}{y})^{1/2} \approx 1 + \frac 1 2 (\frac l y)$$
And, in the limit $y >> l$ we have:
$$ (1+\frac{l}{y})^{1/2} \approx 1$$