MigMRF
- 15
- 0
So I'm trying to figure out how to model a ball getting thrown vertically with the starting velocity v_0. So I've come up with a differential equation which I'm pretty sure is correct:
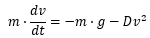
Where D is a constant. So far so good. My problem is solving this. This is my attempt:
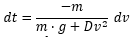
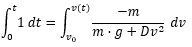
And when i do this and isolate v(t) i get this:
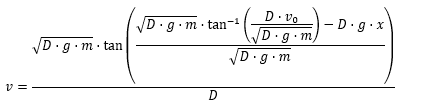
First of all, can anyone confirm this? It should only be used between t=0 and when the graph cross the x-axis. Secondly: Is there another waay to solve this.
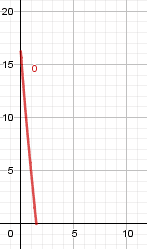
BTW. if anyone were curios the fuction looks like this (for m=0.05 D=0.00085 g=9.82 v_0=16)
Where D is a constant. So far so good. My problem is solving this. This is my attempt:
And when i do this and isolate v(t) i get this:
First of all, can anyone confirm this? It should only be used between t=0 and when the graph cross the x-axis. Secondly: Is there another waay to solve this.
BTW. if anyone were curios the fuction looks like this (for m=0.05 D=0.00085 g=9.82 v_0=16)
Last edited by a moderator: