Where Do the Graphs of |3x-2| and 1/x Intersect and Diverge?

In summary, to determine where the graph of |3x-2| lies below the graph of 1/x, we can set up two different equations and find their intersection point. The solution is when 0<x<1. For the inequality |x+1|-|4x-2|>0, we can break it down into three different cases and find the overlapping intervals where the inequality is satisfied. The final solution is 1/5<x<1. There may be some simplifications and corrections needed in the workings, but the overall method is correct. As for solving modulus inequalities, there may be multiple methods and it may depend on the specific inequality at hand. It is always important to double check the graph and solution
  • #1
AN630078
242
25
Homework Statement
Hello, I have been doing some further work on composite transformations, specifically solving equations and inequalities involving the modulus function. I have not actually been taught how to solve modulus inequalities but have found a method of doing so. In my textbook there are some exercises which I have tried to solve, and I was wondering whether anyone could evaluate my workings to see whether I have used an appropriate method. I am rather uncertain of my solutions so I would greatly appreciate any possible improvements I could implement.

By drawing a sketch of suitable graphs, or otherwise, find the sets of values for x which;

1. |3x-2|<1/x
2. |x+1|-|4x-2|>0
Relevant Equations
|3x-2|<1/x
|x+1|-|4x-2|>0
1. I think the question is asking where is the graph of |3x-2| below the graph of 1/x.
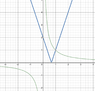
To sketch the graph of y= |3x-2| draw the line of y=3x-2 and reflect the section with negative y-values in the x-axis. Alternatively, I could set 3x-2 ≥0, meaning |3x-2|=3x-2 so draw the line of y=3x-2. Then find 3x-2≤0, meaning |3x-2|=-(3x-2)=2-3x so draw the line of y=2-3x.
Then plot the graph of y=1/x and find the point of intersection between the modulus graph and y=1/x.
This is equivalent to asking where does the modulus of 3x-2 meets the curve y=1/x;
|3x-2|=1/x
The critical values are 0 and 2/3
Consider three situations:
When x<0, rewrite |3x-2|<1/x as -(3x-2)=1/x
-(3x-2)x=1
-3x^2+2x-1=0
Evaluating the discriminant of the quadratic; b^2-4ac=-8
Since the discriminant is negative this indicates that the solutions are not real numbers, since the discriminant cannot be negative for x ∈ ℝ
So there is no solution for x<0.

When 0<x<2/3 rewrite |3x-2|<1/x as -(3x-2)<1/x
-3x+2-1/x<0
3x^2-2x+1/x>0
x>0
Combine the intervals x>0 and 0<x<2/3, the solution is 0<x<2/3

When x>2/3, rewrite |3x-2|<1/x as 3x-2<1/x
3x-2<1/x
3x^2-2x-1<0
Factor this to find the solution, (3x+1)(x-1)
Thus, x=-1/3 or x=1
x<-1/3 or 0<x<1
Combine the intervals x<-1/3, 0<x<1 and x>2/3, the solution is 2/3<x<1
Combining all three regions we see that the inequality is satisfied
when: 0<x<2/3 or 2/3<x<1
So the solution is 0<x<1

One is also able to evaluate this by sketching both of the graphs. The point of intersection is found to be (1,1). Since the graph of y=1/x has a horizontal asymptote of y=0, meaning when x is negative the graph of y=1/x is below the graph of y= |3x-2|

Therefore, combining the solutions to find the set of values for which |3x-2|<1/x this would be when 0<x<1.

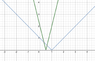
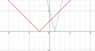
2. |x+1|-|4x-2|>0
Which is equivalent to;|x+1|>|4x-2|
The critical values are -1 and 1/2.
Consider three situations; x<-1
When x<-1, rewrite |x+1|>|4x-2| as -(x+1)>-(4x-2)
-x-1>-4x+2
-x>-4x+3
3x>3
Combining the intervals x>1 and x<0 demonstrates there is no solution.
Consider the second situation; -1<x<1/2
When -1<x<1/2, rewrite |x+1|>|4x-2| as (x+1)>-(4x-2)
x+1>-4x+2
x>-4x+1
5x>1
x>1/5
So the inequality is true for all x>1/5
Merge the overlapping intervals x>1/5 and -1<x<1/2, thus 1/5<x<1/2
Consider the third situation; x>1/2
When x>1/2, rewrite |x+1|>|4x-2| as (x+1)>(4x-2)
x+1>4x-2
x>4x-3
3x<3
x<1
So the inequality is true for all x<1
Merge the overlapping intervals x>1/2 and x<1, thus 1/2<x<1
Combining all three regions we see that the inequality is satisfied
when: 1/5<x<1/2 or 1/2<x<1
So the solution is 1/5<x<1

Would my method of solving the inequalities be correct, or is there a preferable option instead?
 

Attachments

  • Question 1.png
    Question 1.png
    23.4 KB · Views: 213
  • Question 2.png
    Question 2.png
    19.8 KB · Views: 215
  • Like
Likes Delta2
Physics news on Phys.org
  • #2
For 1 I would start with |3x-2| is nonnegative so |3x-2|<1/x implies x>0.

I didn't follow your reasoning here:
When 0<x<2/3 rewrite |3x-2|<1/x as -(3x-2)<1/x​
-3x+2-1/x<0​
3x^2-2x+1/x>0​
x>0​
Is the third line supposed to be 3x^2-2x+1>0?
Write the LHS as 2x^2+(x^2-2x+1).

In this sequence
3x^2-2x-1<0​
Factor this to find the solution, (3x+1)(x-1)​
Thus, x=-1/3 or x=1​
x<-1/3 or 0<x<1​
Shouldn't the last line read "x>-1/3 and x<1"?

For 2, your graph is wrong.
 
  • Like
Likes AN630078
  • #3
haruspex said:
For 1 I would start with |3x-2| is nonnegative so |3x-2|<1/x implies x>0.

I didn't follow your reasoning here:
When 0<x<2/3 rewrite |3x-2|<1/x as -(3x-2)<1/x​
-3x+2-1/x<0​
3x^2-2x+1/x>0​
x>0​
Is the third line supposed to be 3x^2-2x+1>0?
Write the LHS as 2x^2+(x^2-2x+1).

In this sequence
3x^2-2x-1<0​
Factor this to find the solution, (3x+1)(x-1)​
Thus, x=-1/3 or x=1​
x<-1/3 or 0<x<1​
Shouldn't the last line read "x>-1/3 and x<1"?

For 2, your graph is wrong.
Thank you for your reply. For 1, yes sorry my workings should simplify -3x+2-1/x<0 by converting to a fractional form;
-3xx/x+2x/x-1/x<0
-3x^2+2x-1/x<0
Multiply both sides by -1 to reverse the inequality;
3x^2-2x+1/x>0

Combine the intervals x>0 and 0<x<2/3, the solution is 0<x<2/3.

Yes, I think you are correct I should have written x>-1/3 and x<1, but I was trying to identify the regions that satisfy the condition of < 0, being x<-1/3 or 0<x<1.

I have tried to correct my graph for part 2? Sorry, I think I accidentally graphed |x-1| instead of |x+1|?
Besides from this would my workings be correct? Is is there a preferable method to solve modulus inequalities like these instead? 😁
 

Attachments

  • part 2.png
    part 2.png
    14.1 KB · Views: 206
  • #4
Yes, that's the right graph now.
Solving nonlinear inequalities does tend to be messy, often needing to be broken down into cases. Graphing is certainly helpful in guiding you.
There can be quicker ad hoc methods. In the second question you could have written it as (x+1)2>(4x-2)2.
This quickly simplifies to (5x-1)(x-1)<0, whence 1/5<x<1.
 
  • Like
Likes AN630078
  • #5
haruspex said:
Yes, that's the right graph now.
Solving nonlinear inequalities does tend to be messy, often needing to be broken down into cases. Graphing is certainly helpful in guiding you.
There can be quicker ad hoc methods. In the second question you could have written it as (x+1)2>(4x-2)2.
This quickly simplifies to (5x-1)(x-1)<0, whence 1/5<x<1.
Thank you for your reply. Yes, I found found that with nonlinear inequalities. Graphs certainly have been helpful to my understanding this topic better. Although, I still find it a little confusing.
Thank you for your suggestion for the alternative method of solving the second part to this problem, I found that very helpful and less time consuming!
😁
 

1. What are modulus inequalities?

Modulus inequalities are mathematical expressions that involve the absolute value of a variable or expression. They are used to represent the distance of a number from zero on a number line.

2. How do you solve modulus inequalities?

To solve a modulus inequality, you need to isolate the absolute value expression and then split the inequality into two separate inequalities. One inequality will have the positive form of the absolute value expression, and the other will have the negative form. Solve both inequalities separately and then combine the solutions to get the final solution.

3. What is the difference between modulus inequalities and regular inequalities?

The main difference between modulus inequalities and regular inequalities is that modulus inequalities involve the absolute value of a variable or expression, while regular inequalities do not. Modulus inequalities can also have two solutions, one for the positive form and one for the negative form, while regular inequalities typically only have one solution.

4. When are modulus inequalities commonly used?

Modulus inequalities are commonly used in mathematical and scientific applications, such as physics and engineering. They are also used in economics and finance to represent constraints or limits on certain variables.

5. Can you provide an example of solving a modulus inequality?

Sure, for the inequality |x-3| < 5, we would first isolate the absolute value expression to get -5 < x-3 < 5. Then, we split it into two inequalities: -5 < x-3 and x-3 < 5. Solving each separately, we get -2 < x and x < 8. Combining the solutions, we get -2 < x < 8. Therefore, the solution for the original inequality is -2 < x < 8.

Similar threads

Show that if ##x>1##, ##\log_e\sqrt{x^2-1}=\log_ex-\dfrac{1}{2x^2}-##
    • Precalculus Mathematics Homework Help
Replies
8
Views
295
Factor Theorem and Trigonometric Equations Help
    • Precalculus Mathematics Homework Help
Replies
1
Views
1K
Solving a nested logarithmic equation
    • Precalculus Mathematics Homework Help
Replies
2
Views
710
How Do You Solve Complex Absolute Value Inequalities?
    • Precalculus Mathematics Homework Help
Replies
4
Views
1K
Obtain the two incongruent solutions modulo 210 of the system
    • Precalculus Mathematics Homework Help
Replies
7
Views
2K
If ##x> 1## and ##x^2 <2##, prove ##x < y##, ##y^2<2##
    • Precalculus Mathematics Homework Help
Replies
10
Views
1K
Solve the Modulus equation
    • Precalculus Mathematics Homework Help
Replies
1
Views
941
What is the solution to (1+x+x^2+x^3)^2 from Gelfand's Algebra?
    • Precalculus Mathematics Homework Help
Replies
2
Views
1K
Is there a rule that states that I should not divide in this scenario?
    • Precalculus Mathematics Homework Help
Replies
10
Views
613
Solving a modulus inequality in ##x##
    • Precalculus Mathematics Homework Help
Replies
16
Views
1K

Hot Threads

Recent Insights

Back
Top