- #1
dinospamoni
- 92
- 0
Homework Statement
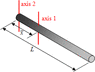
The thin rod shown has a length L = 100 cm, and a density that varies from 26 g/cm at the origin to 3 g/cm at the far end. Determine a) the moment of inertia about axis 1 (passing through the center of mass of the rod), and b) the moment of inertia about axis 2 (passing through the heavy end of the rod).
picture attached
Homework Equations
I already found
Mass of rod = 1.45*10^3 g
Center of mass of rod = 36.8 cm from the more dense end
The density as a function of position I found to be: ρ(x)=.23x + 3
The Attempt at a Solution
For the first part:
I used I = ∫ r^2 * m/L dr
where -36.8 < r < 63.2
and got 1.46*10^6 g*cm^2
For the second part I know it has to do with the parallel axis theorem:
I = I_cm+mh^2
where h = 36.78 cm
and got 3.4*10^6 but that's not right.
Any ideas?
Attachments
Last edited: