Moment of inertia of a bar with two spheres

[duplaimp]

Homework Statement

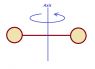
A dumbbell has two spheres of radius 0.10m and mass 10kg (each). The two spheres are connected using a bar with length 1.0m and mass 12kg.
What is the moment of inertia of the dumbbell about an axis perpendicular to an axis at the bar's center of mass?
Moment of inertia of a sphere through its center of mass: \frac{2}{5}MR^{2}
Moment of inertia of a bar through its center of mass: \frac{2}{12}ML^{2}

The Attempt at a Solution

I tried the following:
(sphere) Ip = Icm + Md^{2} <=> Ip = \frac{2}{5} MR^{2} + M(\frac{L}{2} + R)^2 <=> Ip = \frac{7}{5} M R^{2} + M\frac{L^{2}}{4}
(bar) I = \frac{2}{12} ML^{2}

Then I multiplied Ip by 2 and sum I (of the bar). Itotal = 2Ip + I

But the value I am getting is wrong. What I am doing wrong?

 

[TSny]

Hello.

I'm not sure I understand the phrase "about an axis perpendicular to an axis at the bar's center".

But I did note a couple of things.

$(\frac{L}{2} + R)^2 \neq \frac{L^2}{4}+R^2$

Are you sure the moment of inertia of a rod has a factor of 2/12?

 

[SteamKing]

Instead of writing equations off the cuff as it were, set up the problem in an organized manner.

Item      Mass      C.O.M.     Moment   M*Dist^2    MMOI
                    Dist.

Sphere 1   10        0.55        5.5       3.03     (2/5)MR^2
Sphere 2   10       -0.55       -5.5       3.03     (2/5)MR^2
Bar        12         0.0        0.0       0.0      ML^2/12
----------------------------------------------------------
Totals

Add up the totals for each column and use the Parallel Axis Theorem
To find the MMOI for the bar bell.

 

[duplaimp]

Hello.

I'm not sure I understand the phrase "about an axis perpendicular to an axis at the bar's center".

But I did note a couple of things.

$(\frac{L}{2} + R)^2 \neq \frac{L^2}{4}+R^2$

Are you sure the moment of inertia of a rod has a factor of 2/12?

Oops.. The factor is 1/12 and I was thinking in (L*R)^{2} instead of (L+R)^{2}

So, trying again I've got the right result but am I doing it right?

I did this:

(sphere) Ip = Icm + Md^{2} <=> Ip = \frac{2}{5} MR^{2} + M(\frac{L}{2} + R)^2 <=> Ip = \frac{2}{5} M R^{2} + M(\frac{L^{2}}{4}+2\frac{LR}{2}+R^{2})
(bar) I = \frac{1}{12} ML^{2}

Then plugged in the values of each, multiplied I of sphere by two and did a sum of I of bar and I of sphere. Is this correct?

 

[duplaimp]

Hello.

I'm not sure I understand the phrase "about an axis perpendicular to an axis at the bar's center".

But I did note a couple of things.

$(\frac{L}{2} + R)^2 \neq \frac{L^2}{4}+R^2$

Are you sure the moment of inertia of a rod has a factor of 2/12?

Oops.. The factor is 1/12 and I was thinking in (L*R)^{2} instead of (L+R)^{2}

So, trying again I've got the right result but am I doing it right?

I did this:

(sphere) Ip = Icm + Md^{2} <=> Ip = \frac{2}{5} MR^{2} + M(\frac{L}{2} + R)^2 <=> Ip = \frac{2}{5} M R^{2} + M(\frac{L^{2}}{4}+2\frac{LR}{2}+R^{2})
(bar) I = \frac{1}{12} ML^{2}

Then plugged in the values of each, multiplied I of sphere by two and did a sum of I of bar and I of sphere. Is this correct?

 

[TSny]

Yes, that looks correct assuming the axis of rotation is as shown.

I would probably not bother to expand out the $(\frac{L}{2}+R)^2$, but just leave it as $I_p = \frac{2}{5} MR^{2} + M(\frac{L}{2} + R)^2$. The expression is more compact that way and it will be easier to evaluate numerically.

 

[duplaimp]

The axis of rotation is as you shown. Thank you!