Moment of inertia of a disc using rods as differential elements

[Hamiltonian]

Homework Statement

find the moment of inertia of a disc using rods of variable lengths as differential element.(axis perpendicular to plane of disc and through its COM)

Relevant Equations

-

I know there are more convenient differential elements that can be chosen to compute the moment of inertia of a disc(like rings).

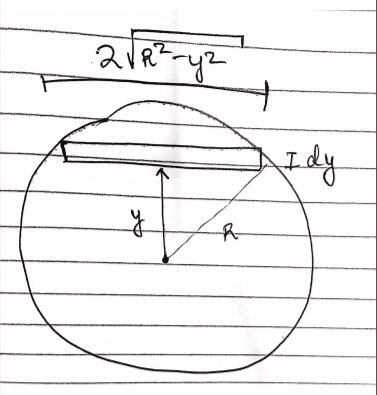
the mass of the differential element:
$$dm = (M/\pi R^2) (dA) = (M/ \pi R^2) (2\sqrt{R^2 - y^2})(dy)$$
the moment of inertia of a rod through its COM is $(1/12)ML^2$ hency by applying the parallel axis theorem :
$$dI = (1/12)(dm)(2\sqrt{R^2 - y^2})^2 + (dm)y^2$$
$$I = (\frac{2M}{3\pi R^2})\int_{-R}^{+R} (R^2 + 2y^2)\sqrt{R^2 - y^2}(dy) $$
$$I = (5/12)MR^2$$
where am I going wrong?

 

[TSny]

Looks like you set it up correctly. Are you sure you evaluated the integral correctly?

 

[Orodruin]

I agree with @TSny , the integral is not correctly performed.

 

[Hamiltonian]

Looks like you set it up correctly. Are you sure you evaluated the integral correctly?

$$I = (\frac{2M}{3\pi R^2})\int_{-R}^{+R} (R^2 + 2y^2)\sqrt{R^2 - y^2}(dy) $$
$$I = (\frac{2M}{3\pi R^2})\int_{-R}^{+R} (R^2\sqrt{R^2 - y^2} + 2y^2\sqrt{R^2 - y^2} ) (dy) $$

$$I = \frac{2M}{3\pi R^2} [R^2 (\frac{\pi R^2}{2}) + 2(\frac{\pi R^4}{8})] = (1/2)MR^2 $$
i used wolfram alpha to do it now i am getting the correct answer thanks!

 

[haruspex]

$$I = (\frac{2M}{3\pi R^2})\int_{-R}^{+R} (R^2 + 2y^2)\sqrt{R^2 - y^2}(dy) $$
$$I = (\frac{2M}{3\pi R^2})\int_{-R}^{+R} (R^2\sqrt{R^2 - y^2} + 2y^2\sqrt{R^2 - y^2} ) (dy) $$

$$I = \frac{2M}{3\pi R^2} [R^2 (\frac{\pi R^2}{2}) + 2(\frac{\pi R^4}{8})] = (1/2)MR^2 $$
i used wolfram alpha to do it now i am getting the correct answer thanks!

Note that solving the integral involves a trig substitution which effectively converts it to having chosen the more sensible differential element in the first place. Is that a useful exercise?
Perhaps it is a lesson that when a trig substitution helps with an integral one should consider what it means in terms of the original analysis.

 

[Steve4Physics]

Note that solving the integral involves a trig substitution which effectively converts it to having chosen the more sensible differential element in the first place. Is that a useful exercise?
Perhaps it is a lesson that when a trig substitution helps with an integral one should consider what it means in terms of the original analysis.

The original homework statement specifically requires use of "rods of variable lengths as differential element".

Is there a better approach than that used by the OP? Am I missing something obvious?

Edited - typo'.

 

[Hamiltonian]

The original homework statement specifically requires use of "rods of variable lengths as differential element".

Is there a better approach than that used by the OP? Am I missing something obvious?

Edited - typo'.

you could use the differentiable elements as rings.

$$dm = \frac{M}{\pi R^2} 2\pi x dx$$
the moment of inertia of a ring is $= MR^2$
$$dI = (dm)x^2$$
$$I = \int_0^R \frac{M}{\pi R^2} 2\pi x^3 dx$$
$$I = (1/2)MR^2$$
the resulting integral is much simpler in this case

 

[Steve4Physics]

you could use the differentiable elements as rings.

$$dm = \frac{M}{\pi R^2} 2\pi x dx$$
the moment of inertia of a ring is $= MR^2$
$$dI = (dm)x^2$$
$$I = \int_0^R \frac{M}{\pi R^2} 2\pi x^3 dx$$
$$I = (1/2)MR^2$$
the resulting integral is much simpler in this case

Yes, I know! (And in Post #1, you'd already mentioned that you realized this.)

But the original homework asks for an analysis in terms of 'rods'. Whoever set the homework specifically didn't want you to use rings - presumably to make the exercise a little more demanding.

I was pointing out that your method is the only one (as faras I can see) that properly answers the original question. So don't be tempted to hand-in a solution based on the ring method, except perhaps as an addendum to demonstrate that you know that this is better approach.

 

[haruspex]

The original homework statement specifically requires use of "rods of variable lengths as differential element".

Is there a better approach than that used by the OP? Am I missing something obvious?

Edited - typo'.

I'm sure the OP approach satisfies the given requirement in the way the setter expected. Just pointing out that the algebra can't help but switch to the standard route under the covers. I don't think there's a way to avoid it.