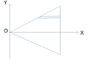
- #1
Who_w
- 3
- 2
- Homework Statement
- Calculate the moment of inertia of a triangle relatively OY
- Relevant Equations
- Given the height of the triangle
Please, I need help! I need to calculate the moment of inertia of a triangle relatively OY. I have an idea to split my triangle into rods and use Huygens-Steiner theorem, but after discussed this exercise with my friend, I have a question: which of these splits are right (picture 1 and 2)? Or maybe my idea is wrong?