Moment of Inertia of an L-shaped bar

[Kotten]

Homework Statement

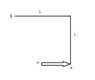
The L-shaped bar of mass m is lying on the horizontal surface when the force P is applied at A as shown. Determine the initial acceleration of point A. Neglect friction and the thickness of the bar.
(Sorry, don´t know how to get you a better picture)

L
B----------------
I
I L
I
P--------> I
A

Homework Equations

G=1/M*Sum(m_i*r_i) (a)
Sum(F_x)=ma_(Gx) (b)
Sum(F_y)=ma_(Gy) (c)
Sum(M_G)=I_G*alpha (d)

The Attempt at a Solution

I have calculated the center of mass, using eq (a), and got (from the bend of the bar)
G= -L/4 i -L/4 j
I also used eq (b) to get
P=ma_(Gx) ---> a_(Gx)=P/m
(c) gave
0=ma_(Gy) ---> a_(Gy)=0
and from (d) i got
P*3/4*L=I_G*alpha ---> alpha=(3PL)/(4*I_G )
And then I guess I have to calculate the moment of inertia for the figure, but I don´t know how to do that :/ Also I´m a bit confused, because this seems to me like a way to solve this problem, the chapter on how to calculate momento of inertia comes after this in the book. Is there another way to solve it? Or is this wrong and I´m missing something?

 

[Doc Al]

(Sorry, don´t know how to get you a better picture)

Use the "whiteboard" feature to create a diagram. Then you can cut and paste it into your post.

 

[Kotten]

Thank you :)

 

[Doc Al]

And then I guess I have to calculate the moment of inertia for the figure, but I don´t know how to do that :/ Also I´m a bit confused, because this seems to me like a way to solve this problem, the chapter on how to calculate momento of inertia comes after this in the book. Is there another way to solve it? Or is this wrong and I´m missing something?

It's not obvious to me how you'd solve it without first calculating the moment of inertia. I guess you'll have to read the next chapter! Hint: treat the L-shape as two straight rods.

 

[Kotten]

Ok, thank you :)
I have now tried to calculate the moment of inertia:
I_GA=1/12*m/2*L^2
I_GB=--------II---------
That would give (using Steiners Theorem):
I_G=I_GA+m/2*(L/4)^2+I_GB+m/2*(L/4)^2=2(1/12*m/2*L^2+m/2(L/4)^2)=L^2*m(1/12+1/16)
I got the moment about G:
M_G=-Pkx(-1/4*Li+3/4*Lj)=1/4PL(3i+j)
And then I used that to get:
alpha=M_G/I_G=(PL(3i+j))/(4*L^2*m(1/12+1/16))=(P(3i+j))/(Lm(1/3+1/4))
But after that I´m not sure how to continue... I´ve got the acceleration of point O, and the angular acceleration, but how do I calculate the acceleration of A without knowing the angular velocity?

 

[Doc Al]

But after that I´m not sure how to continue... I´ve got the acceleration of point O, and the angular acceleration, but how do I calculate the acceleration of A without knowing the angular velocity?

Hint: They ask for the initial acceleration.