Moment of inertia of the body Question

[Kishor Bhat]

Homework Statement

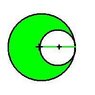
A hole of radius R/2 is cut from a solid sphere of radius R. If the mass of the remaining plate is M, then moment of inertia of the body about an axis through the centre is____.

Answer:57/140*M*R^2

Homework Equations

Moment of inertia of solid sphere is (2/5)*M*R^2

The Attempt at a Solution

I was thinking that we could find the moment of inertia of the initial body, then subtract the MI of the removed part. However, the fact that the mass of removed part is not specified is hindering my progress. I do not know how else to approach the problem.

 

[ehild]

You can assume that the whole sphere has the same density.

ehild

 

[Kishor Bhat]

So the approach is correct?

 

[ehild]

So the approach is correct?

Yes, go ahead.

ehild

 

[Kishor Bhat]

It works! Thanks a lot. In retrospect, I realize that the question really wasn't that hard. But thanks anyway. :)

 

[NascentOxygen]

It works! Thanks a lot. In retrospect, I realize that the question really wasn't that hard. But thanks anyway. :)

It wasn't difficult?? Here I was thinking it looked to be two exercises in calculus, and you went and did it in your head? How did you do it?

 

[Kishor Bhat]

Okay.. let's assume the density of the material of the sphere is D. So the mass of the whole sphere is M'= D*4/3*pi*R^3. The mass of the part which is cut out would then be D*4/3*pi*(R/2)^3 since it's radius is half that of the sphere.
By calculating the volumes of the two, we can find that the smaller sphere (cut out) constitutes 1/8th of the total mass. So M (mass of remaining part) is therefore 7/8th of total mass M'. In turn, M'=(8/7)*M.
Similarly, mass of cut out sphere in terms of M is (1/7)*M. Using the MI equation, we get:
[(2/5)*(8/7)*M*R^2]-[(2/5)*(1/7)*M*(R/2)^2]=(62/140)*M*R^2.

The answer is slightly off, isn't it. Ergh. It might be a printing mistake. Or have I done something blatantly wrong?

 

[NascentOxygen]

A "hole" in a sphere, or a "hollow" sphere. So you saw the problem as a sphere being hollowed out? I saw it as an apple corer being pushed through an apple, creating a hole all the way through it.

Was the question dictated to you, so although the person may have said a sphere is made "hollow", you wrote it down as a "hole" is made in a sphere?

hole/hollow, they sound a bit similar.

And the mass of the remaining "plate"? Is this the term the book used?

 

[ehild]

NascentOxygen is right, do you know the shape of that hole and where it is positioned inside the sphere?
If it is really a sphere your approach is correct if the hole is concentric with the big sphere. But it would be difficult to cut a sphere inside the big one in this way! The hole looks rather like the one in the picture, the centre of the small sphere is at distance R/2 from the centre of the big one. But then the MI of the small sphere has to be calculated with respect to the axis through the centre of the big sphere. Apply the Parallel Axis Theorem.

ehild

 

[Kishor Bhat]

It just says hole in the question. As for position, I've attached the jpg file.

 

[Kishor Bhat]

Seeing as how I can't see it anywhere, here goes: the diagram is basically two circles, with the smaller's circumference touching the larger one's. Like in common tangents, when the smaller circle is inside the larger.

 

[ehild]

I edited my last post. Read it. Your calculation is not correct.

ehild

 

[Kishor Bhat]

Oh yeah... whenever we add or subtract MI's it has to be about the same axis right? Epic fail on my part. Thanks again.

 

[ehild]

Oh yeah... whenever we add or subtract MI's it has to be about the same axis right? Epic fail on my part. Thanks again.

Yes, they have to be about the same axis.


ehild

 

[NascentOxygen]

Whether it's a spherical void inside a sphere, or a circular piece cut from metal plate, I think it's reasonable to assume it is centred, if we have to assume anything. The fact that the question says "remaining plate" suggests circles and holes, more than spheres and hollows.

I think MI would be maximised if the void was centred, in any case.

 

[Kishor Bhat]

Mm I'll try 'em out. Thanks a bunch. Both of you. I think we can conclude: Case closed. :)

 

[NascentOxygen]

Seeing as how I can't see it anywhere, here goes: the diagram is basically two circles, with the smaller's circumference touching the larger one's. Like in common tangents, when the smaller circle is inside the larger.

Oh, so it's not necessarily a "hole"? The word "hole" wasn't mentioned in the book? That is a word you came up with to describe a spherical void inside the sphere?

And what about the word "plate"? Is that quoted from the book, or is that your word also?

Which brings into question the word "sphere". Does the book actually say "sphere"? Maybe it really is a disc, a circle of metal plate?

 

[Kishor Bhat]

Nope. All words were directly from the worksheet.

 

[ehild]

Anyway, the given result corresponds to a sphere of radius R with a spherical hole or void or opening or ...(I do not know the correct word being not a native English) of radius R/2 and centre at R/2 distance from that of the big sphere. "Plate" is not the correct word for the remaining body, but it does not matter. An Indian and a Hungarian understand each other's English.

ehild

 

[Kishor Bhat]

Truer words have not been spoken. :P

 

[SammyS]

The remaining "part" ?

 

[ehild]

The remaining "part" ?

Yes. it could have been "part" originally, and mistyped at the end.
Is there any word for a solid body, which is not a sphere, not a cube, not a block, not a pyramid, but somewhat irregular ? Is the word "body" correct?

ehild