Momentum and Impulse Problem with a Ball bouncing off a Wall

[GiantGoose]

Homework Statement

See attached.
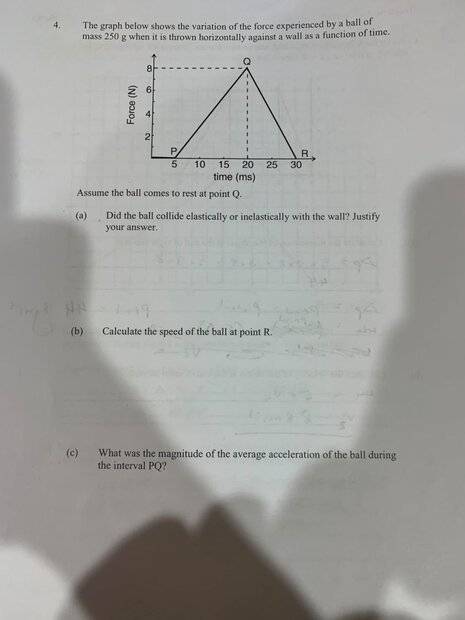
Graph shows variation of force experienced by ball of 250g mass when thrown against a wall. Comes to rest at point Q.
a) Did the ball collide elastically or inelastically with the wall? Justify.
b) Calculate the speed of the ball at point R
c) What was the magnitude of the average acceleration of the ball during the interval PQ?

Relevant Equations

F=ma
change in momentum = final - initial
change in momentum = force x time

a) Assuming it is inelastic as it is accelerating and therefore kinetic energy is not conserved? Intuitively this doesn't feel right...

b) change in momentum = p initial - p final = force x time
p initial = 0 as at rest
p final = 0.25 x v2
force x time = area under graph = 0.1
therefore 0.25 x v2 = 0.1
v2 = 0.4 ms-1

c) After google searching I have discovered that acceleration is the area under the graph of a f against t graph, but I am certain I have not been taught this. Is there are more intuitive way to figure this out?

Many thanks!

 

[BvU]

Hello @GiantGoose,
$\qquad$ !

Homework Statement:: See attached.
Graph shows ...

Unfortunately it's illegible...

https://www.physicsforums.com/threads/homework-help-guidelines-for-students-and-helpers.686781/

$\$

 

[jbriggs444]

a) Assuming it is inelastic as it is accelerating and therefore kinetic energy is not conserved? Intuitively this doesn't feel right...

Yes, that is incorrect.

A bouncing ball will experience acceleration. The bounce can be either elastic (equal kinetic energy before and after the bounce) or inelastic (unequal kinetic energy before and after the bounce).

b) change in momentum = p initial - p final = force x time

That would be correct for a constant force. Here we have a force that varies over time. That calls for integration (area under the curve) rather than simple multiplication.

c) After google searching I have discovered that acceleration is the area under the graph of a f against t graph

No. That is not correct.

Instantaneous acceleration is given by $a = F/m$. This is Newton's second law.

The area under the graph of f against t gives you the change in momentum. If you want average acceleration, you need to divide change in velocity by the time interval over which that change occurs.

Note that change in momentum is useful information because it will help you answer part a).

 

[Orodruin]

a) Assuming it is inelastic as it is accelerating and therefore kinetic energy is not conserved? Intuitively this doesn't feel right...

This is indeed not sufficient. During the collision, energy can be stored up as potential energy in deformation of the ball etc. You will need to find a different line of argument here. What is significative of an elastic collision of an object with an immovable object (such as a wall)?

p initial = 0 as at rest

Why would the ball be at rest initially? It is being thrown against the wall.

I may be missing something here as your image is really low quality and it is difficult to see what it actually says.

c) After google searching I have discovered that acceleration is the area under the graph of a f against t graph, but I am certain I have not been taught this. Is there are more intuitive way to figure this out?

Then you should not trust your googling skills. The area under an F-t-graph is the total impulse during the considered time, not the acceleration.

 

[GiantGoose]

Thanks for the help. These are the answers I have come to, but i am still not certain about part (a), are they correct, and if not where am I going wrong?

Many Thanks again!

 

[jbriggs444]

It would be more polite and rules-conforming if you were to transcribe your chicken scratching into text.

$\Delta p = 0.06 N$?
A change in momentum does not have units of force. It has units of force times time. Or mass times velocity.

I stopped reading after that.

 

[haruspex]

Thanks for the help. These are the answers I have come to, but i am still not certain about part (a), are they correct, and if not where am I going wrong?

View attachment 300699View attachment 300700

Many Thanks again!

Per forum rules, images are for diagrams and textbook extracts. Posting your working as images makes it hard for us to refer to parts of it.

You calculated two changes in momentum (quoting the wrong units) but gave them the same name, $\Delta p$. That leads to confusion.

You noted these two changes in moment are different and concluded that the velocity had changed. I hope that is not exactly what you meant.
Momentum and velocity are vectors, so even in one dimension the sign matters. Had the collision been perfectly elastic, would you expect the velocities to be the same?
Is it possible for a mass to undergo two different momentum changes yet end up with unchanged velocity?

In (c), you have two errors.
You have two velocities, zero and -0.24m/s. In (v-u)/t, which is u and which is v?
Then how did -0.24 turn into +24?

 

[erobz]

Now I'm confused, what am I missing?

For "part a"
I don't think we can show this. If the collision is perfectly elastic, then we expect the change in momentum to be $2 m v_P$

This implies to answer the question we have to compare:

$$ \int_{\rm{5 ms}}^{\rm{20ms}} F_{PQ} \, dt + \int_{ \rm{20 ms}}^{\rm{30 ms} } F_{QR} \, dt < 2 m v_P $$

But, we don't know the momentum of the ball before the collision? Unless I'm missing it in the picture somewhere.

and for the same reasons we can't calculate "part b" either?

 

[haruspex]

we don't know the momentum of the ball before the collision?

We are told the ball is instantaneously at rest at point Q.

 

[erobz]

We are told the ball is instantaneously at rest at point Q.

Oh...I didn't see that. I realized that must be the case, but it didn't click for some reason to use that fact to find the initial momentum.