SUMMARY
The discussion centers on the relationship between the translation operator and the momentum operator in quantum mechanics. It establishes that the momentum along the x-axis is represented by the derivative operator with respect to x, as per the Stone-von Neumann uniqueness theorem. The translation operator is defined as &hat;U(\vec{\xi})=\exp(\mathrm{i} &hat{\vec{p}} \cdot \vec{\xi}), which acts on a wave function by shifting its position. This leads to the conclusion that the momentum operator in the position representation is given by &hat{\vec{p}}=-\mathrm{i} \vec{\nabla}.
PREREQUISITES
- Quantum mechanics fundamentals
- Understanding of operators in quantum mechanics
- Familiarity with the Stone-von Neumann uniqueness theorem
- Basic knowledge of wave functions and their representations
NEXT STEPS
- Study the Stone-von Neumann uniqueness theorem in detail
- Learn about the mathematical derivation of the momentum operator in quantum mechanics
- Explore the implications of the translation operator on wave functions
- Investigate the role of the derivative operator in quantum mechanics
USEFUL FOR
Students and professionals in quantum mechanics, physicists focusing on operator theory, and anyone interested in the mathematical foundations of quantum physics.

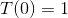 and
and